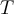Hola Manuel.
Te dicen que la TL es una simetría respecto de un plano, de modo que vamos a pensarlo en términos geométricos, visualmente por así decir.
Lo primero es ver que si un vector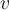 pertenece al plano
pertenece al plano 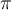 , entonces
, entonces  , de modo que todo el plano está formado por vec.p. asociados a
, de modo que todo el plano está formado por vec.p. asociados a  . Esto ya nos dice que
. Esto ya nos dice que  .
.
Te dicen que la TL es una simetría respecto de un plano, de modo que vamos a pensarlo en términos geométricos, visualmente por así decir.
Lo primero es ver que si un vector
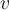 pertenece al plano
pertenece al plano 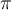 , entonces
, entonces  , de modo que todo el plano está formado por vec.p. asociados a
, de modo que todo el plano está formado por vec.p. asociados a  . Esto ya nos dice que
. Esto ya nos dice que  .
.Esto nos dice que la recta que pasa por el origen y es perpendicular al plano 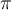 es
es  , que tiene dimensión 1.
, que tiene dimensión 1.
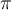 es
es  , que tiene dimensión 1.
, que tiene dimensión 1.Entonces podemos armar una base de vec.p., dos vectores LI del plano y uno de la recta perpendicular.
Respecto del determinante, recuerda que dos matrices asociadas al mismo operador (pero en distintos pares de bases,) son semejantes.
El otro enfoque es hallar la expresión analítica (la "fórmula") para 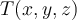 y luego hallar los valores propios, etc.
y luego hallar los valores propios, etc.
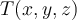 y luego hallar los valores propios, etc.
y luego hallar los valores propios, etc.Espero haber sido de ayuda.
Saludos
J.