Buenas, quería consultar como se puede resolver este ejercicio. Tengo una idea de como encararlo pero no logro resolverlo. Gracias!

Buenas, quería consultar como se puede resolver este ejercicio. Tengo una idea de como encararlo pero no logro resolverlo. Gracias!

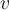 pertenece al plano
pertenece al plano 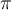 , entonces
, entonces  , de modo que todo el plano está formado por vec.p. asociados a
, de modo que todo el plano está formado por vec.p. asociados a  . Esto ya nos dice que
. Esto ya nos dice que  .
.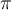 es
es  , que tiene dimensión 1.
, que tiene dimensión 1.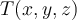 y luego hallar los valores propios, etc.
y luego hallar los valores propios, etc.