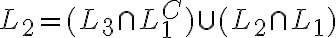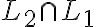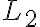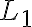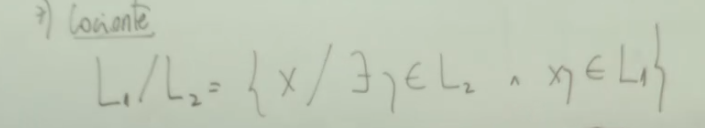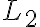[Ejercicio 1] [Parte 4]

[Ejercicio 1] [Parte 4]

de Leandro Pereira Modzelewski -
Número de respuestas: 9

Buenas, quería saber si mi razonamiento para este ejercicio está bien. 

L2 se puede expresar como L2 = (L3 intersección L1 complemento) U (L2 intersección L1)

De donde la primera parte es regular ya que L3 es regular, L1 es finito por ende es regular, su complemento lo es, y la intersección de regulares es regular. 

Mi duda entra sobre la segunda parte, ya que creo que no puedo hacer ninguna afirmación acerca de L2 intersección L1 sin tener información extra, por lo que creo que la afirmación sería falsa al no poder generalizar. Si L2 intersección L1 fuera vacío sería verdadera, pero si no lo es va a depender del conjunto que formen. 

Agradecería me puedan guiar un poco acerca de si lo que estoy planteando está bien o si se puede realizar alguna otra afirmación con la información dada por el ejercicio ya que quedé un poco trancado con esto.

Muchas gracias,

Leandro.


En respuesta a Leandro Pereira Modzelewski

Re: [Ejercicio 1] [Parte 4]

de Santiago Gongora -
Buenas tardes Leandro,

está bien tu razonamiento sobre la primera parte, lo de que el lenguaje se puede reescribir como L_2 = (L_3 \cap L_1^C) \cup (L_2 \cap L_1) y lo de que L_3 \cap L_1^C es regular por propiedades. Como decías, lo que te está faltando para terminar la demostración es ver qué pasa con   L_2 \cap L_1 . Como también (bien) dijiste, sobre L_2 no podés afirmar nada porque es lo que estás tratando de probar.

Sin embargo, lo que sí sabés es que L_1 es finito....

...¿Y qué pasa cuando hacemos la intersección de cualquier conjunto con un conjunto finito? ¿Puede pasar que ese conjunto resultante sea infinito?

Acordate que antes dijiste que si un conjunto es finito, entonces es regular. Y eso está bien de bien.

Contame si pudiste liquidarlo.
Saludos,
Santi
En respuesta a Santiago Gongora

Re: [Ejercicio 1] [Parte 4]

de Leandro Pereira Modzelewski -
Buenas Santiago,

Gracias por la pronta respuesta,

Ahora sí me quedó claro como rematarlo. Como L1 es finito, la intersección de L2 con L1 también será finita, por ende será regular y entonces sumado a lo que ya razoné anteriormente, como la unión de regulares es regular, concluyo que L2 es regular. Sería así no?

Muchas gracias,
Leandro.
En respuesta a Leandro Pereira Modzelewski

Re: [Ejercicio 1] [Parte 4]

de Santiago Gongora -
Ahí está. Por definición, el resultado de A intersección B es siempre un subconjunto de A y también un subconjunto de B. Como A es finito, una intersección donde él participe va a dar siempre como resultado un conjunto finito.

Bueno, listo :D

Cualquier cosa a las órdenes.
Santi
En respuesta a Santiago Gongora

Re: [Ejercicio 1] [Parte 4]

de Rodrigo Mira Martinez -
Buenas,
Otra forma de verlo podría ser con el cociente de conjuntos? Como tenemos L3 regular, y L1 es finito. Y como L3\L1 = L2, entonces sería regular.
Estaría bien así?
Saludos.
En respuesta a Rodrigo Mira Martinez

Re: [Ejercicio 1] [Parte 4]

de Santiago Gongora -
Buen día Rodrigo,

la definición que da Juanjo del cociente en el teórico es esta:
Definicion de cociente dada en openfing

El cociente tiene que ver con la concatenación. Da como resultados los strings que al concatenarles al final una tira de L_2 , dan como resultado una tira de L_1 .

¿Cómo lo aplicarías en este caso?

Saludos,
Santi
En respuesta a Santiago Gongora

Re: [Ejercicio 1] [Parte 4]

de Bruno Emanuel Gandos Telis -
Hola Santi, a mí se me ocurrió la siguiente demostración por absurdo. No sé si es correcta.
Supongo por absurdo que L2 no es regular, entonces no existirá una expresión regular r2 tal que L2 = L(r2). Ahora, por hipótesis sabemos que L3 es regular entonces existe una expresión regular r3 tal que L3 = L(r3), a su vez, como L1 finito => L1 regular => existe una expresión regular r1 tal que L1 = L(r1).
Como L3 = L1 U L2, aplicando la primera clausula inductiva de la definición de expresiones regulares obtengo que r3 = r1 | r2 con r1 y r2 ER para L1 y L2. Llegando así a un absurdo.

El único paso que me genera dudas en la demostración es en la construcción de r3. Según la definición, si L1 = L(r1) y L2 = L(r2) => r3 = r1 | r2, al ser esto un implica no se si puedo asumir lo que asumí, ya que bajo mi suposición no existe la expresión r2.
Muchas gracias.
Saludos.
En respuesta a Bruno Emanuel Gandos Telis

Re: [Ejercicio 1] [Parte 4]

de Santiago Gongora -

Buen día Bruno,

el problema es el que decís, que estás suponiendo que L_2 no es regular, entonces no podés "agarrarte" de la clausura de la unión.

Algo tangencial a esto, que siempre tienen que tener en mente, es que el hecho que la unión sea cerrada para los lenguajes regulares, no quiere decir que un lenguaje regular unido a un lenguaje no regular no pueda dar un lenguaje regular. Dicho de otra manera, puede pasar que: Reg \cup NoReg = Reg . El problema de este asunto es que no podés asegurar qué pasa de antemano en la unión de un lenguaje regular y otro no regular, sin conocer los lenguajes.

Y en eso, entiendo, es que se te complica la demostración.

Disculpá si no fui más en detalle con la demostración, pero como comentó Juanjo en el EVA no solemos corregir ejercicios porque si lo hacemos con uno lo tenemos que hacer con todos, y lleva un tiempo muy grande. Agrego, como comentario personal, que encuentro positivo que ustedes mismos logren entender en su mente qué cosas son las que le generan dudas de la solución (como vos hiciste, sospechando que algo andaba mal con la construción de r_3 ).

Cualquier otra duda que te venga, preguntá :D

Saludos,
Santi

PD: Si les parece raro lo de Reg \cup NoReg = Reg , piensen qué pasa si el lenguaje regular en cuestión es \Sigma^* :)