Estuve un buen rato pensando el este ejercicio pero no me salió. ¿Me pueden dar una idea para poder hacerlo?
hola:
aquí la idea es pensar "a futuro" con la ayuda de un autómata no determinista.
por ejemplo, tomemos una tira x de entrada que nosotros queremos que evalúe en "a".
supongamos que empieza por "a", luego x = a.y -> a , ¿en cuánto debe evaluar "y" para que "a.y" valga "a"? mirando la tabla, existen dos posibilidades, que "y" evalúe en "a" o que lo haga en "b". observen que a.a = a.b = a. ahora el problema ya no es "quiero que x evalúe en a" sino que el resto y evalúe en "a" o "b", lo que no es un problema porque se puede modelar usando no determinismo.
¿qué sucede si en lugar de con "a", x empieza por "b"? el único valor que sirve para y de forma tal que b.y = a es solamente b.
¿y si x empieza por "c"? en este caso, el resultado de "y" debe valer "c" para que c.c = a.
entonces, construimos un autómata en donde cada estado qX representa "quiero que la tira evalúe en x".
luego, por lo que vimos arriba, g(qA.a) = {qA, qB...}, g(qA,b) ={qB} y g(qA,c) = {qC}
de la misma forma, por poner algún ejemplo más, g(qB,a) = { } y g(qC,b) = {qA}
¿por qué los puntos suspensivos? porque me estaría faltando la condición de aceptación, pero lo dejo para que lo piensen un poco más.
saludos,
d.-
aquí la idea es pensar "a futuro" con la ayuda de un autómata no determinista.
por ejemplo, tomemos una tira x de entrada que nosotros queremos que evalúe en "a".
supongamos que empieza por "a", luego x = a.y -> a , ¿en cuánto debe evaluar "y" para que "a.y" valga "a"? mirando la tabla, existen dos posibilidades, que "y" evalúe en "a" o que lo haga en "b". observen que a.a = a.b = a. ahora el problema ya no es "quiero que x evalúe en a" sino que el resto y evalúe en "a" o "b", lo que no es un problema porque se puede modelar usando no determinismo.
¿qué sucede si en lugar de con "a", x empieza por "b"? el único valor que sirve para y de forma tal que b.y = a es solamente b.
¿y si x empieza por "c"? en este caso, el resultado de "y" debe valer "c" para que c.c = a.
entonces, construimos un autómata en donde cada estado qX representa "quiero que la tira evalúe en x".
luego, por lo que vimos arriba, g(qA.a) = {qA, qB...}, g(qA,b) ={qB} y g(qA,c) = {qC}
de la misma forma, por poner algún ejemplo más, g(qB,a) = { } y g(qC,b) = {qA}
¿por qué los puntos suspensivos? porque me estaría faltando la condición de aceptación, pero lo dejo para que lo piensen un poco más.
saludos,
d.-
Buenas!
Espero se encuentren muy bien.
Me está costando muchísimo entender esta parte y la explicación. Entiendo cómo separa los casos y qué tiene que venir después de cada símbolo para que dé "a", pero al momento de hacer la función me confunde, porque pienso en leer el símbolo que está inmediatamente después, y ahí es como si aplicara asociativa de izquierda a derecha, por lo que no estaría bien.
Agradezco si me pueden dar una mano.
Saludos!
Espero se encuentren muy bien.
Me está costando muchísimo entender esta parte y la explicación. Entiendo cómo separa los casos y qué tiene que venir después de cada símbolo para que dé "a", pero al momento de hacer la función me confunde, porque pienso en leer el símbolo que está inmediatamente después, y ahí es como si aplicara asociativa de izquierda a derecha, por lo que no estaría bien.
Agradezco si me pueden dar una mano.
Saludos!
Hola,
va otra explicación a ver si ayuda. Uso # para el operador.
va otra explicación a ver si ayuda. Uso # para el operador.
Vamos a considerar tres estados que los vamos a llamar: tira_que_evalua_en_a, tira_que_evalua_en_b y tira_que_evalua_en_c.
Para cada uno de estos estados vamos a suponer que tiene la semántica que refleja su nombre, es decir, el estado tira_que_evalua_en_a refiere a las tiras que a partiendo de él evaluan en a.
Para pensar las transiciones del primero, tira_que_evalua_en_a, mirando la tabla buscamos las operaciones que tienen como resultado a.
Tenemos por ejemplo que a#a=a, o sea que a#tira_que_evalua_en_a=a, entonces hacemos una transición desde tira_que_evalua_en_a hacia sí mismo con una a.
También tenemos que a#b=a, o sea que a#tira_que_evalua_en_b=a, entonces hacemos una transición desde tira_que_evalua_en_a hacia tira_que_evalua_en_b con una a.
Repetimos esto para el resto de operaciones que tienen como resultado a, agregando las transiciones que salen del estado tira_que_evalua_en_a. Con el mismo razonamiento agregamos transiciones que parten de tira_que_evalua_en_b y tira_que_evalua_en_c.
Queda para pensar estado incial y final.
Saludos
Buenas! Estuve viendo este ejercicio y a decir verdad me llevó bastante tiempo entenderlo, dejo lo que pude hacer.
El estado inicial que tomé fue qA, porque al inicio aún no he leído nada y quiero que mi tira evalúe en a, sin embargo hice pruebas y al parecer el estado final debe ser qB pero no tengo explicación alguna de porque se da esto.
El estado inicial que tomé fue qA, porque al inicio aún no he leído nada y quiero que mi tira evalúe en a, sin embargo hice pruebas y al parecer el estado final debe ser qB pero no tengo explicación alguna de porque se da esto.
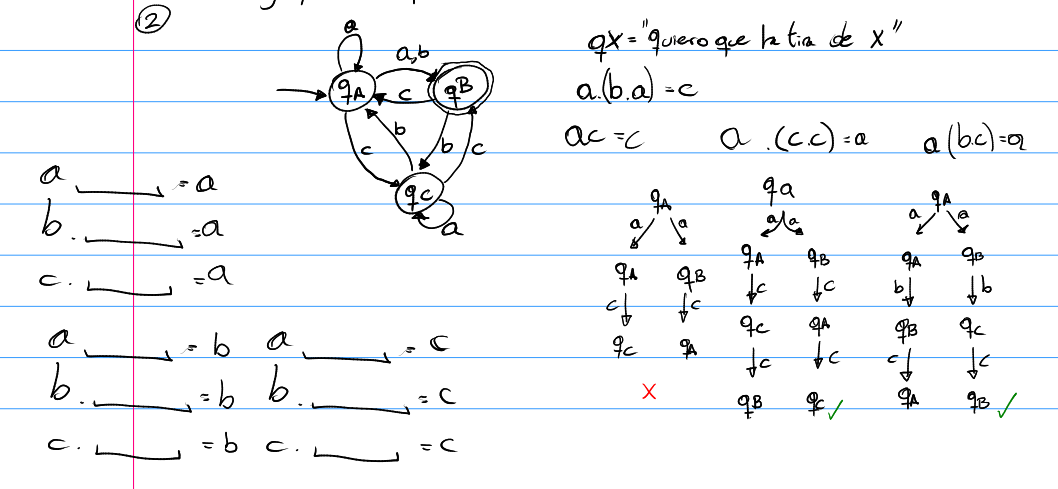
Estimado, como ya habíamos aclarado, en el foro no se van a corregir ejercicios o parte de ejercicios.
Para eso están las clases de consulta de los jueves, que son justamente para eso.
Sobre la marcha evaluaremos que si fuera necesario agregamos alguna instancia de consulta virtual por parte del equipo docente.
Espero sepan comprender.
Saludos
Juanjo
Para eso están las clases de consulta de los jueves, que son justamente para eso.
Sobre la marcha evaluaremos que si fuera necesario agregamos alguna instancia de consulta virtual por parte del equipo docente.
Espero sepan comprender.
Saludos
Juanjo
