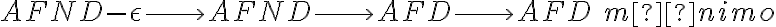Buenas, quería saber si la idea de este ejercicio es aplicar los algoritmos que vimos en clase para pasar de un AFND o AFND-ε a un AFD o si la mejor manera de resolverlo es pensando qué tiras reconoce el autómata dado y a partir de eso pensar en un AFD que reconozca las mismas tiras.
Hasta ahora venía resolviéndolo de la segunda manera porque creo que el autómata puede quedar más sencillo de esta forma. Con la única parte que tuve problema fue con la 2 porque no pude darme cuenta cuál es el lenguaje asociado al autómata.
Pensé en algunas expresiones regulares que juntas podrían definir este lenguaje:
- las tiras de ceros y unos de la forma 0(10)* (por las transiciones de p a s y de s a p)
- las tiras de ceros y unos que no tienen más de 2 ceros consecutivos y terminan en (0|1)1* o en (0|1)1*(0|1)0 (por el resto de las transiciones (entre p, q, r y s))
Pero no se si esto está bien ni si me están faltando algunas tiras. Además, no pude encontrar una ER que defina al lenguaje completo.
Les agradezco si me pueden ayudar!