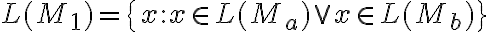Buenas, en la parte 1, estaria bien pensar al conjunto M1 como el conjunto formado por la union de los alfabetos, los estados finales, 
las funciones de transicion, etc. junto con el super estado qo que contiene a qoa y qob?
Buen día Guzman,
si entendí bien lo que planteás, estás re bien encaminado.
La idea de esta parte es que piensen cómo se deben relacionar los autómatas cuando el lenguaje pedido es la unión de los lenguajes que ellos reconocen. Así que reformulándolo un poquito:
Entonces bastaría con que uno de los dos autómatas la reconozca, lo que es equivalente a decir que basta con que la tira a reconocer vaya por un camino que la conduzca a la máquina ya existente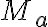 
o a la ya existente 
.
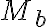Observá también que en la letra dice que el autómata tiene que ser finito, pero no dice nada sobre su determinismo. Así que capaz para estos ejercicios te pueda venir bien usar algo del no determinismo...como las transiciones épsilon :) Usando transiciones épsilon desde un estado inicial general, vas a poder moverte a una u otra máquina y el resto se cuenta solo porque las máquinas 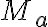y 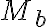ya están dadas por letra.
Sobre lo que comentás del superestado que contemple los dos estados iniciales, también se podría hacer. En el caso de que usen el mismo alfabeto muy probablemente se generaría un no determinismo, por lo que estaríamos en la misma situación de la transición épsilon: la solución es un autómata finito no determinista.
Intenté guiarte sin spoilear tanto, aunque un poquitititito sí :P...pero cualquier duda volvés a preguntar ¿sí? :D
Saludos,
Santi
La union es relativamente simple, y el complemento es trivial... Pero la interseccion no tiene la misma simplicidad, sinceramente, no se ni por donde encararlo. ¿Alguna pista?
Tomando el ejemplo de los AFD de la parte B, no se me ocurre como armar un AF que me diga si una tira tiene largo multiplo de 6 a partir de dos que me dicen si es de largo par y multiplo de 3 respectivamente.
Hola Rodolfo,
primero he de opinar que no creo que el complemento sea trivial, pero sí sencillo. Es un resultado sorprendente que sea tan fácil reconocer el complemento de un lenguaje regular ¿no? :D
Con respecto a lo otro: de acuerdísimo en que computar la intersección es la parte más difícil del ejercicio. Te tiro un centro a ver si te encamino y, si no, volvés a preguntar ¿sí?
Tenemos dos autómatas donde cada uno reconoce tiras que pertenecen a sus respectivos lenguajes. Lo que queremos lograr es que una tira que se ingrese en el nuevo autómata pueda cumplir con los flujos de cómputo de ambos autómatas, desde el inicio hasta el final.
Es decir, entonces, la idea es que la tira recorra los dos autómatas a la vez, por lo que vas a tener que crear "superestados" que representen que la tira siendo computada está en el estado "x" del primer autómata y en el "y" del segundo...y después, la tira es aceptada si... :P
Ya sabés, a las órdenes.
Saludos,
Santi
Ok... es horripilante, pero lo entendí... Me pongo a trabajar en un producto de Q_a y Q_b y debería salir...
Funcionó, muchas gracias
hola:
tal vez sea horripilante, pero es una forma algorítmica de crear un autómata para la intersección. de esta forma, si uno tiene un problema más complejo, puede "partirlo" en propiedades más simples, crear los autómatas finitos correspondientes y un algoritmo calcula el autómata que clasifica aquellas tiras que cumplen todas esas propiedades.
en realidad, esta "forma de pensar" sirve también para crear cosas más complejas o resolver viejos problemas de nuevas formas... por ejemplo, se puede crear un algoritmo para el cálculo de un AF determinista para la unión de lenguajes sin pasar por un AFND... es la misma idea cambiando únicamente el conjunto de estados finales...
saludos,
d.-
Ah buenísimo que haya salido, Rodolfo :D
Y suscribo al mensaje de Diego. Es un ejercicio medio complicado pero da una herramienta tremenda para pensar los problemas, al igual que el de pensar el complemento.
Cualquier cosa a las órdenes.
Santi
Y suscribo al mensaje de Diego. Es un ejercicio medio complicado pero da una herramienta tremenda para pensar los problemas, al igual que el de pensar el complemento.
Cualquier cosa a las órdenes.
Santi