Consultas de pruebas anteriores

Buenas

El ejercicio plantea funciones continuas con dominio $[0,2]$ por tanto, por Weierstrass tienen que tener máximo y mínimo.

Sea $f:[0,2] \to (0,5)$ continua, por Weierstrass f tiene máximo y mínimo, notemos $a = \min\{f(x) : x \in [0,2]\}$, $b = \max\{f(x) : x \in [0,2]\}$.

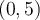Como el codomino de $f$ es $(0,5)$ entonces $a \in (0,5)$ y $b\in (0,5)$. Es decir $0< a \leq b < 5$

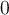En particular $p = \frac{a}{2}$ verifica que $0$ (es decir esta en el intervalo 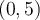$(0,5)$) y no esta en la imagen de $f$ (pues es menor al mínimo) por tanto $f$ no puede ser sobreyectiva.

En esencia el ejercicio dice que la imagen de esta función no puede ser un intervalo abierto.

Saludos