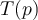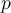GAL2-1S: Ejercicio 18

Hola. Buenas noches. Intentando encarar el ejercicio me he encontrado con alguna duda de interpretación para la selección de los posibles pasos a seguir. El camino que pensé para la resolución del ejercicio incluía lo siguiente:

- Evaluar el polinomio genérico p con cada uno de los elementos de la base canónica de R2[t], B: (1, T+1, (T+1)^2), con la finalidad de determinar cuál sería el T(p) para cada uno de ellos con los valores de a, b y c, los cuales dependerán del término que acompañe a la t; todo esto con la finalidad de posteriormente dar con sus coordenadas en la base canónica de R4 (A) y obtener la matriz asociada a esas bases. Pasa que cuando llego a la evaluación de p con (T+1)^2, me encuentro que al sustituir ese valor en la fórmula del polinomio genérico me quedaría un exponente de t^4, lo cual no me resulta coherente con el análisis que realicé.

Supongo que debo estar errando en la manera de interpretar el ejercicio, por lo que agradecería alguna idea para su resolución.

Re: Ejercicio 18

de Tabare Nahuel Roland Silveira - lunes, 20 de marzo de 2023, 14:34

Buenas.

La base canónica de

$\mathbb{R}_2[t]$ es

$\{ 1,t,t^2\}$ . Para hallar la matriz asociada, a

$T$ , lo primero que tenés que hacer es calcular

$T(p)$ para cada

$p$ en la base canónica. Se tiene que

$T(a+bt+ct^2) = (2a + 3b − 8c, a + b + c, 4a − 5c, 6b)$ . Luego, podemos calcular

$T(1)$ : tenemos que observar que

$1 = 1 (1) + 0(t) + 0(t^2)$ , es decir, es

$a=1,b=0,c=0$ , por lo que

$T(1) = (2,1,4,0)$ . Si ahora querés calcular

$T(t),$ se tiene que

$t = 0 (1) + 1 (t) + 0 (t^2)$ , es decir,

$a=0,b=1,c=0$ , con lo que

$T(t) = (3,1,0,6)$ , y así podés seguir con los demás.

Para la parte 2, lo que cambia es la base de la que partís, pero la idea es similar. Por ejemplo, uno de los vectores de la base es

$(t-1)^2 = 1 - 2t +t^2$ , de donde de acuerdo a la notación del parrafo anterior resulta

$a=1,b=-2,c=1$ . Luego

$T(2-6-8, 1 -2 +1, 4 -5, -12 )$ . Repitiendo la misma idea con los demás vectores de la base, podés obtener la matriz asociada.

Espero que eso aclare un poco el ejercicio.

Saludos!