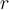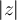Hola, en este ejercicio llegué a que
pero no sé cómo continuar, esto me dio que L=1 así que no puedo saber de forma fácil si es convergente uniformemente en ese disco, ya que si fuera convergente se mantendría la continuidad y capaz con eso se resolvía, pero no sé cómo seguir
de todas formas tendría que probar que ya de por sí log sea continua en esa zona, pero no me sirve de nada si no es convergente uniforme ya que si converge pero puntualmente podría no conservarse la continuidad







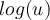

![log_{(-\pi,\pi]}(u) log_{(-\pi,\pi]}(u)](https://eva.fing.edu.uy/filter/tex/pix.php/8f2b6ede9bf2b60be3dd7d126244b80c.png)