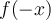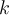5.b demo

5.b demo

de Nataly Melanie Ruber Maimo -
Número de respuestas: 1

Hola, me quedó esta demo sin resolver, no sé qué estoy haciendo mal pero no logro que quede

en primer lugar anoté que si f es par f(z)=f(-z) y si es impar f(-z)=-f(z)

luego 

f(z)= \sum_{n=0}^{ \infty }a_{n}(z)^{n}=a_{0}+a_{1}z+a_{2}z^{2}+...a_{n}(z)^{n}

y luego lo derivé varias veces para ver cómo se veía

en el caso de que f sea par, por ejemplo, f(z) se veía así:

f(z)= \sum_{n=0}^{ \infty }a_{n}(-z)^{n}=a_{0}-a_{1}z+a_{2}z^{2}-a_{3}z^{3}...a_{n}(-z)^{n}

de aquí pude ver que los términos con n impares llevan un -. Luego al hacer la derivada segunda, eran los términos con n par los que llevaban el menos, al derivarlo tercera, volvieron a ser lo n impares los que quedaban negativos y así, lo cual cumple una propiedad que dice que la derivada de una función par es impar y la derivada de una función impar es par. Luego se me ocurrió hacer el Taylor ya que tenía algunas derivadas pero no llegué a nada. De la demostración anterior saqué que  a_{n}=f^{n}(z_{0})/n! en este caso z0 sería 0 ya que tiene centro 0. El tema es que no llego a que nada se me anule. Por ejemplo si yo, usando que f es par, busco para n=3

a_{3}=f^{3}(0)/3! = a_{3}6/3!=a_{3} entonces no me da 0 como debería

gracias
En respuesta a Nataly Melanie Ruber Maimo

Re: 5.b demo

de Marcos Martinez Leiranes -
Hola, te contesté en persona pero contesto por acá en caso que alguien más se haya trancado con eso.

Supongamos que f es par, entonces se cumple la siguiente igualdad: \sum_{n=0}^{\infty}a_n z^{n}=f(x)=f(-x)=\sum_{n=0}^{\infty}a_{n} (-z)^{n}.

Si pasamos f(-x) restando entonces tenemos que 0=f(x)-f(-x)=\sum_{k=0}^{\infty}a_{2k+1} z^{2k+1}. En otras palabras llegamos a que la serie de potencia de los impares nos da la función nula, por lo que concluímos que a_{2k+1}=0 para todo k. El caso en que la función es impar es análogo.

Saludos!