Hola.
Un primer comentario, va a haber muchas bases que cumplan lo que pide el ejercicio. Esto es importante en el sentido de que en algún momento vas a tener que elegir vectores que cumplan lo que pide el ejercicio, no va a haber una única solución.
El ejercicio te pide hallar bases y
y  tales que la matriz asociada queda como indica ahí. Para que eso ocurra, entre otras cosas, tiene que pasar que
tales que la matriz asociada queda como indica ahí. Para que eso ocurra, entre otras cosas, tiene que pasar que  , lo que quiere decir que
, lo que quiere decir que 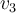 está en el núcleo de
está en el núcleo de  . Además, por como deben quedar las coordenadas de
. Además, por como deben quedar las coordenadas de 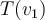 y
y 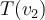 , sabés que
, sabés que 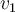 y
y 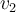 no pueden estar en el núcleo de
no pueden estar en el núcleo de  . Eso te da una idea de como podés tomar
. Eso te da una idea de como podés tomar 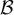 : tenés que tomar tres vectores que formen una base de forma tal que uno de ellos esté en el núcleo y los otros dos no.
: tenés que tomar tres vectores que formen una base de forma tal que uno de ellos esté en el núcleo y los otros dos no.
Por último, fijate que necesitas que , lo que equivale a que
, lo que equivale a que  . Podés hacer un argumento similar con
. Podés hacer un argumento similar con 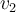 , lo cual te da condiciones que tienen que cumplir los vectores
, lo cual te da condiciones que tienen que cumplir los vectores 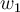 y
y 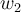 de
de  . El vector
. El vector 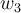 simplemente tiene que verificar que
simplemente tiene que verificar que 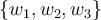 forme una base. Con eso, podés tener una idea de como tomar la base
forme una base. Con eso, podés tener una idea de como tomar la base  de forma de cumplir lo que pide el ejercicio.
de forma de cumplir lo que pide el ejercicio.
Espero que esto ayude a pensar el ejercicio.
Saludos!
Un primer comentario, va a haber muchas bases que cumplan lo que pide el ejercicio. Esto es importante en el sentido de que en algún momento vas a tener que elegir vectores que cumplan lo que pide el ejercicio, no va a haber una única solución.
El ejercicio te pide hallar bases
 y
y  tales que la matriz asociada queda como indica ahí. Para que eso ocurra, entre otras cosas, tiene que pasar que
tales que la matriz asociada queda como indica ahí. Para que eso ocurra, entre otras cosas, tiene que pasar que  , lo que quiere decir que
, lo que quiere decir que 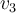 está en el núcleo de
está en el núcleo de  . Además, por como deben quedar las coordenadas de
. Además, por como deben quedar las coordenadas de 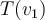 y
y 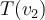 , sabés que
, sabés que 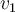 y
y 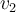 no pueden estar en el núcleo de
no pueden estar en el núcleo de  . Eso te da una idea de como podés tomar
. Eso te da una idea de como podés tomar 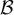 : tenés que tomar tres vectores que formen una base de forma tal que uno de ellos esté en el núcleo y los otros dos no.
: tenés que tomar tres vectores que formen una base de forma tal que uno de ellos esté en el núcleo y los otros dos no.Por último, fijate que necesitas que
 , lo que equivale a que
, lo que equivale a que  . Podés hacer un argumento similar con
. Podés hacer un argumento similar con 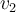 , lo cual te da condiciones que tienen que cumplir los vectores
, lo cual te da condiciones que tienen que cumplir los vectores 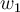 y
y 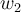 de
de  . El vector
. El vector 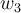 simplemente tiene que verificar que
simplemente tiene que verificar que 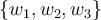 forme una base. Con eso, podés tener una idea de como tomar la base
forme una base. Con eso, podés tener una idea de como tomar la base  de forma de cumplir lo que pide el ejercicio.
de forma de cumplir lo que pide el ejercicio.Espero que esto ayude a pensar el ejercicio.
Saludos!