Hola,
La idea de lo que hiciste está bien. Tan solo recordá que en el ejercicio, la matriz de la que partís es , donde
, donde  y
y  son bases que pueden no ser canónicas. Eso quiere decir que el sistema que resolviste, lo que te da son las coordenadas de la imagen de
son bases que pueden no ser canónicas. Eso quiere decir que el sistema que resolviste, lo que te da son las coordenadas de la imagen de  en la base
en la base  . Para obtener la base de
. Para obtener la base de 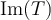 , tenes que deshacer las coordenadas: por ejemplo, el vector
, tenes que deshacer las coordenadas: por ejemplo, el vector  que obtuviste, te da el vector
que obtuviste, te da el vector  , que ese es uno que efectivamente está en la
, que ese es uno que efectivamente está en la 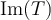 .
.
Sobre la parte 3, lo que te piden son los vecores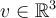 tales que
tales que  . Podemos escribir a
. Podemos escribir a 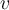 en coordenadas en a base
en coordenadas en a base 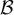 , es decir, escribimos
, es decir, escribimos  . Además,
. Además,  . Por lo tanto, para hallar
. Por lo tanto, para hallar  , podemos resolver el sistema
, podemos resolver el sistema  . Una vez obtenemos
. Una vez obtenemos  , podes obtener
, podes obtener 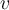 , dado que lo que hallaste son sus coordenadas en la base
, dado que lo que hallaste son sus coordenadas en la base 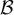 .
.
Espero que eso aclare un poco.
Saludos!
La idea de lo que hiciste está bien. Tan solo recordá que en el ejercicio, la matriz de la que partís es
 , donde
, donde  y
y  son bases que pueden no ser canónicas. Eso quiere decir que el sistema que resolviste, lo que te da son las coordenadas de la imagen de
son bases que pueden no ser canónicas. Eso quiere decir que el sistema que resolviste, lo que te da son las coordenadas de la imagen de  en la base
en la base  . Para obtener la base de
. Para obtener la base de 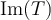 , tenes que deshacer las coordenadas: por ejemplo, el vector
, tenes que deshacer las coordenadas: por ejemplo, el vector  que obtuviste, te da el vector
que obtuviste, te da el vector  , que ese es uno que efectivamente está en la
, que ese es uno que efectivamente está en la 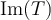 .
.Sobre la parte 3, lo que te piden son los vecores
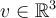 tales que
tales que  . Podemos escribir a
. Podemos escribir a 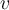 en coordenadas en a base
en coordenadas en a base 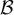 , es decir, escribimos
, es decir, escribimos  . Además,
. Además,  . Por lo tanto, para hallar
. Por lo tanto, para hallar  , podemos resolver el sistema
, podemos resolver el sistema  . Una vez obtenemos
. Una vez obtenemos  , podes obtener
, podes obtener 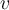 , dado que lo que hallaste son sus coordenadas en la base
, dado que lo que hallaste son sus coordenadas en la base 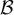 .
.Espero que eso aclare un poco.
Saludos!