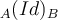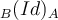Buenos días. Para hacer el ej 14, primero debería elegirme una base A eso va a determinar mi base B. luego con la informacion de mi matriz asociada a(T)b hallo los trasformados de los vctores de mi base B, para luego hallar T y finalmente hallar b(T)a, es correcto ese procedimiento ?
a(T)b es la inversa de b(T)a ?? (T no es la identidad)
Coincido con tu razonamiento aunque no se si esta bien, consulto la misma duda, aunque en cuanto a tu segunda pregunta puedo aportar que generalmente sea T: V -> W (una transformación lineal) un isomorfismo (transformación lineal biyectiva), por el teorema de las dimensiones podemos deducir que el rango de la matriz asociada es n (distinto de 0) por lo que la matriz asociada es invertible, deduciendo lo siguiente [a(T)b]‐¹ = b(T‐¹)a.
Espero haberme explicado correctamente, saludos.
Espero haberme explicado correctamente, saludos.
Buenas, les respondo a ambos.
Un primer comentario, la respuesta del ejercicio no depende de que base elijan.
Nos piden hallar:
donde en la igualdad estamos usando propiedades de la matriz de cambio de base. La matriz del medio,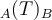
, es la que nos da la letra del ejercicio. Ahora, fíjense que nos dicen que 
y 
; es decir, tenemos las coordenadas de la base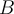 
en la base 
, con lo que podemos calcular la matriz 
. Por último, sabemos que 
es la inversa de , por lo que también podemos hallarla. Es decir, tenemos las tres matrices que necesitábamos para calcular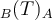 
.
Díganme si esto les ayuda a pensar el ejercicio (quedan por hacer las cuentas).
Saludos!
Un primer comentario, la respuesta del ejercicio no depende de que base elijan.
Nos piden hallar:
donde en la igualdad estamos usando propiedades de la matriz de cambio de base. La matriz del medio,
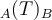, es la que nos da la letra del ejercicio. Ahora, fíjense que nos dicen que y ; es decir, tenemos las coordenadas de la base 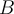en la base , con lo que podemos calcular la matriz . Por último, sabemos que es la inversa de , por lo que también podemos hallarla. Es decir, tenemos las tres matrices que necesitábamos para calcular 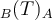.Díganme si esto les ayuda a pensar el ejercicio (quedan por hacer las cuentas).
Saludos!
Buenos días Tabare, muchas gracias por la explicación, me quedo mucho mas claro. ahora, en la primer igualdad de matrices, colocaste dos veces la misma matriz de cambio de base, hay un error allí ? Gracias.
Hola,
La iguadad está bien. Me confundí después cuando puse que tenemos las tres matrices que necesitamos para calculalr 
, solo se necesitan dos: 
y 
. La matriz 
la usamos para hallar 
.
Espero que eso aclare.
Saludos!