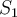Buenas.
La sugerencia que te doy es la siguiente: fijate que como va de
va de  en
en  y no es inyectiva, el teorema de las dimensiones te dice que
y no es inyectiva, el teorema de las dimensiones te dice que 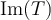 no es todo
no es todo  , por lo que podes definir una transformación
, por lo que podes definir una transformación 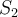 no nula pero que se anule en
no nula pero que se anule en  (por ejemplo, podés tomar una base de la imagen de
(por ejemplo, podés tomar una base de la imagen de  , completarla a una base de
, completarla a una base de  , y definir
, y definir 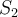 como una transformación que manda los vectores de la base de la imagen al 0, y el resto de vectores de la base a algún vector no nulo de
como una transformación que manda los vectores de la base de la imagen al 0, y el resto de vectores de la base a algún vector no nulo de 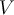 ). ¿Se cumple en este caso que
). ¿Se cumple en este caso que  ?
?
La sugerencia que te doy es la siguiente: fijate que como
 va de
va de  en
en  y no es inyectiva, el teorema de las dimensiones te dice que
y no es inyectiva, el teorema de las dimensiones te dice que 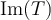 no es todo
no es todo  , por lo que podes definir una transformación
, por lo que podes definir una transformación 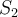 no nula pero que se anule en
no nula pero que se anule en  (por ejemplo, podés tomar una base de la imagen de
(por ejemplo, podés tomar una base de la imagen de  , completarla a una base de
, completarla a una base de  , y definir
, y definir 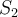 como una transformación que manda los vectores de la base de la imagen al 0, y el resto de vectores de la base a algún vector no nulo de
como una transformación que manda los vectores de la base de la imagen al 0, y el resto de vectores de la base a algún vector no nulo de 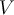 ). ¿Se cumple en este caso que
). ¿Se cumple en este caso que  ?
?