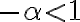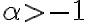Hola buenas, tengo una consulta acerca de este ejercicio. No comprendo como llegar a concluir que la integral impropia se comporta de la misma forma que describe la solución. 
En respuesta a Joaquin Caballero Aldorasi
Re: Examen Julio 2022 - Ejercicio 10
de Bernardo Marenco -
Hola Joaquin. Fijate que si 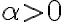 el "problema" de la impropia está en
el "problema" de la impropia está en 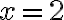 , que es cuando se anula el denominador. En ese punto, el integrando es equivalente a
, que es cuando se anula el denominador. En ese punto, el integrando es equivalente a 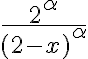 , que, a menos de una constante, se comporta igual que la impropia de
, que, a menos de una constante, se comporta igual que la impropia de 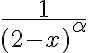 . El caso
. El caso 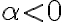 es parecido: en ese caso, como el exponente en el integrando es negativo, es como si tuvieras el cociente "al revés"
es parecido: en ese caso, como el exponente en el integrando es negativo, es como si tuvieras el cociente "al revés" 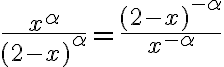 . Entonces ahora el "problema" de la impropia es en
. Entonces ahora el "problema" de la impropia es en 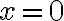 , y el último cociente en
, y el último cociente en 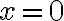 es equivalente a
es equivalente a 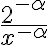 , cuya impropia, a menos de una constante, se comporta como la de
, cuya impropia, a menos de una constante, se comporta como la de 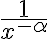 .
.
Saludos
Buenas, tengo una duda en este mismo ejercicio. ¿Cómo determino que para los alfa en (-1,0) tsmbién converge, siendo que para los alfa menores que 0 llego a que converge si −α < 1 es decir si α > 1? Graciaas
Claro, a mi me parecía que cuando dividias en una desigualdad y había cambio de signo era así, osea se invertía la desigualdad pero aún se manternía el cambio de signo, me confundí cuando miré la solución, que está así:


Gracias!
Ah ok, hay un error en la solución entonces.
Saludos
Saludos