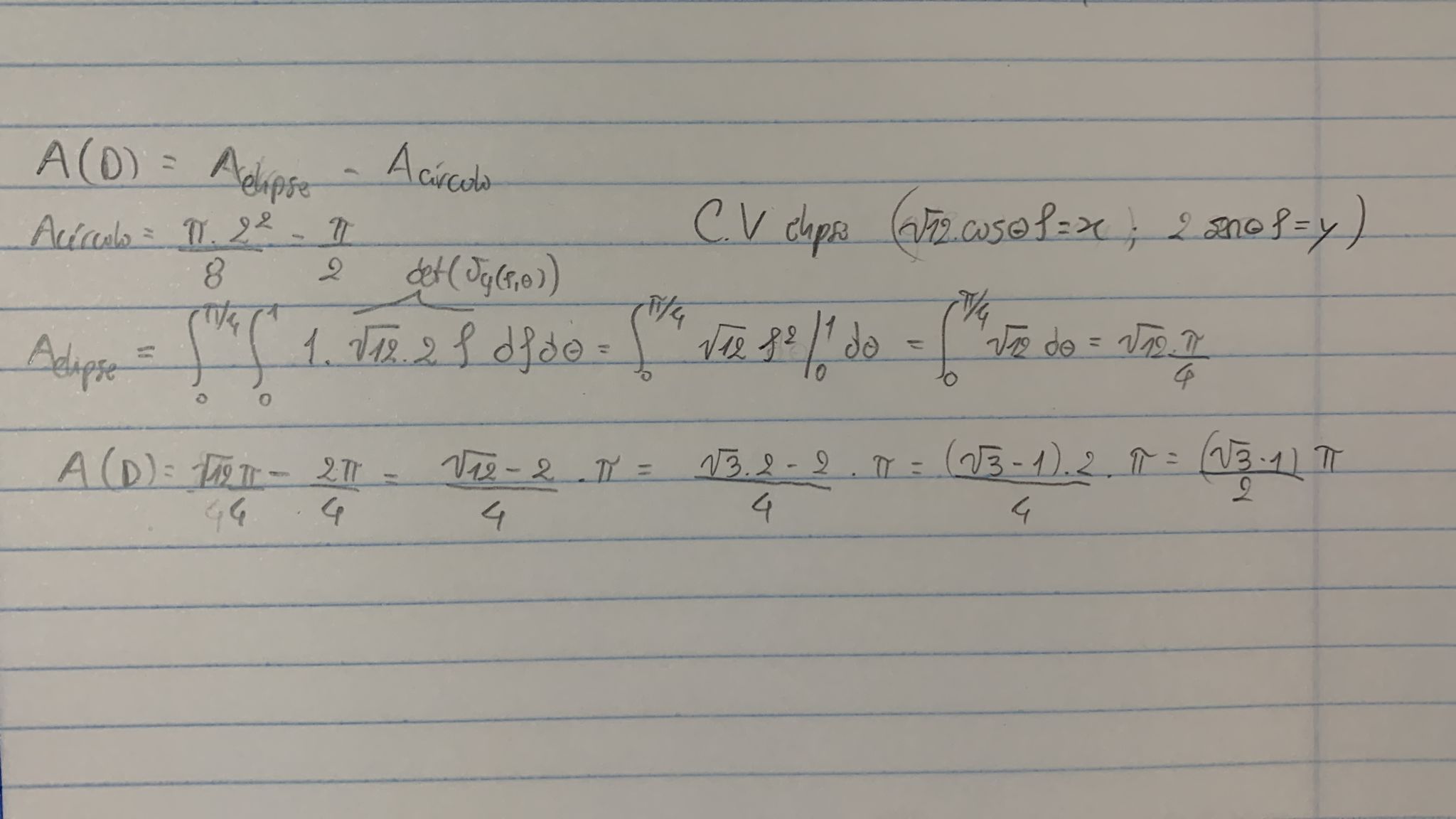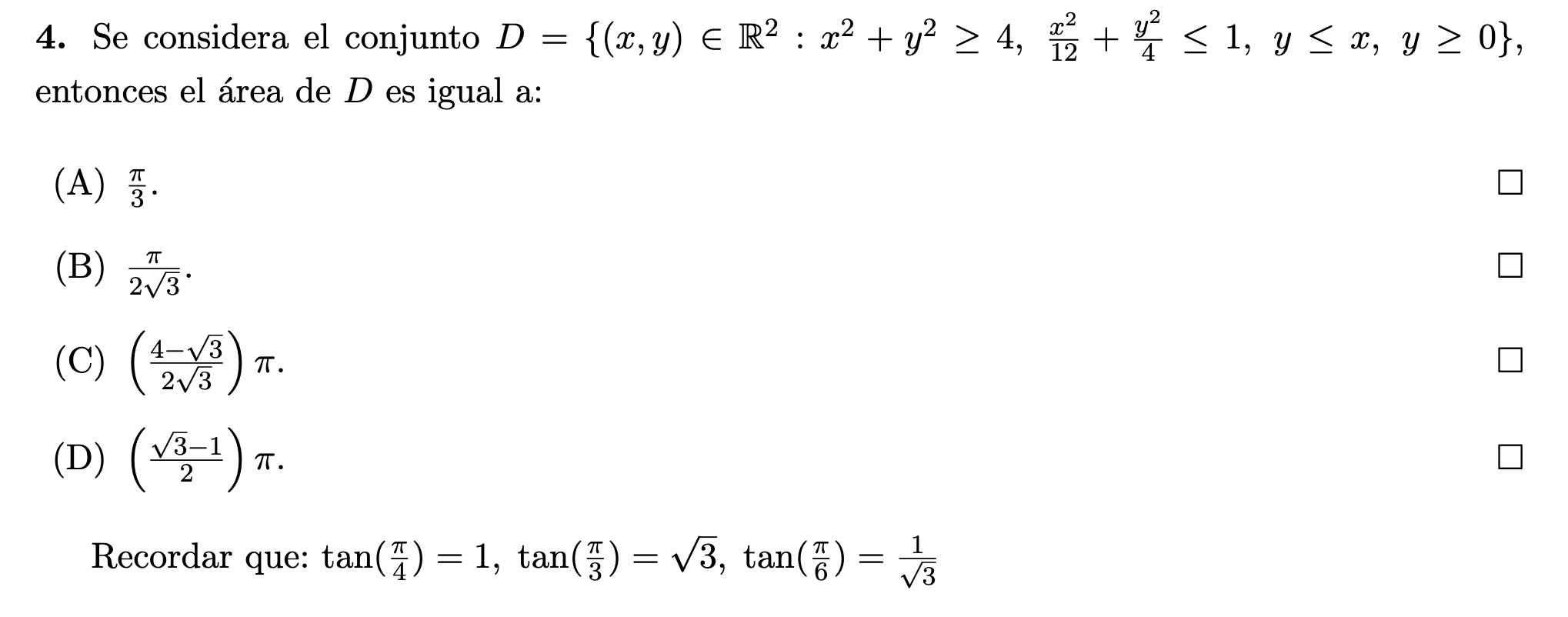
Usando polares, queda lo siguiente:
No sé integrar lo que queda en la integral de afuera.
Haciéndolo sin polares, separo el dominio en dos:
Pero tampoco estoy pudiendo integrar eso.
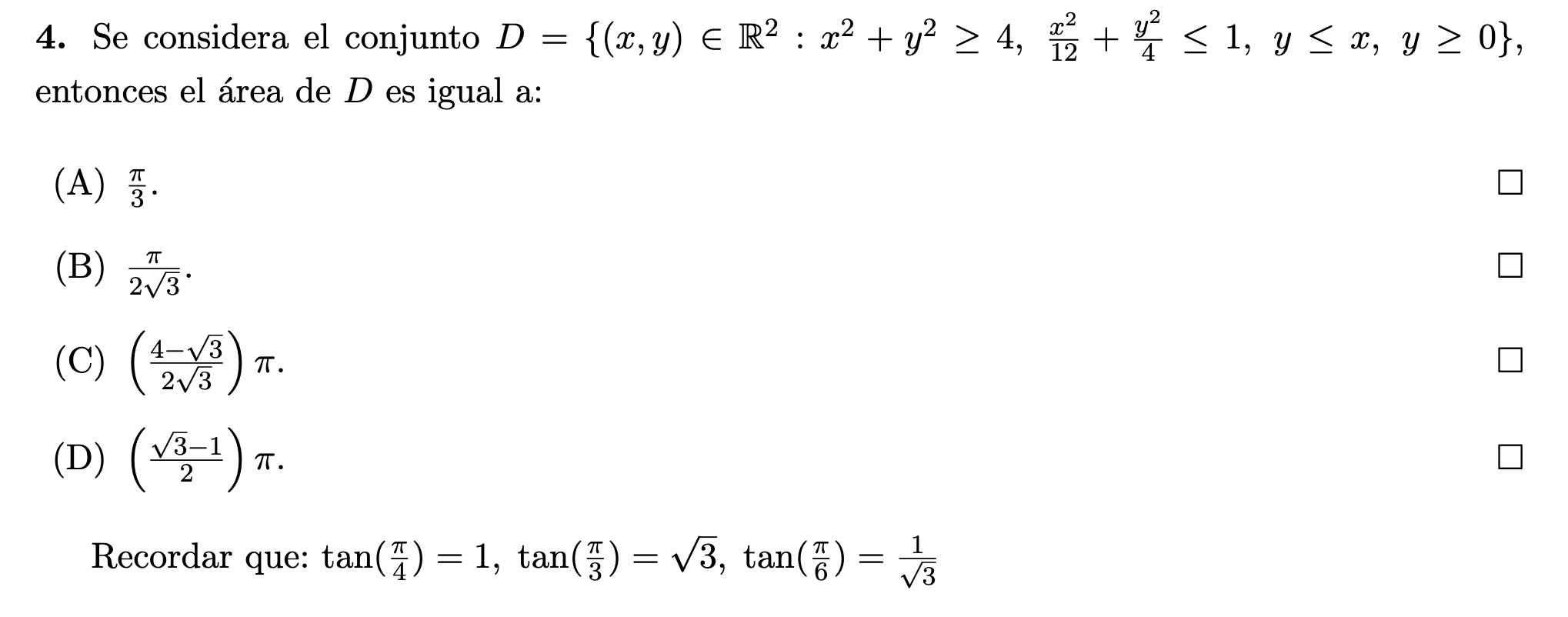
Usando polares, queda lo siguiente:
No sé integrar lo que queda en la integral de afuera.
Haciéndolo sin polares, separo el dominio en dos:
Pero tampoco estoy pudiendo integrar eso.
Buenas!
La forma más fácil es resolver la ecuación que planteaste en polares, la otra es bastante más complicada, esa quedaría:
Ahora la parte complicada es resolver el término de la izquierda, para eso sacamos de factor común 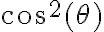 :
:
Ahora podemos aplicar un cambio de variable: 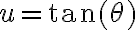 y
y 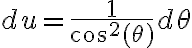 por lo que la integral nos queda:
por lo que la integral nos queda:
Ahora aplicamos otro cambio de variable para tener la primitiva de  con
con 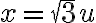 y por lo tanto
y por lo tanto  :
:
Usando los datos que nos da la letra llegamos a que el resultado es:
Saludos!
Florencia
Hola. Lo que planteás no está mal, es otro posible camino para resolverlo. El resultado al que llegues debería ser el mismo.
Saludos