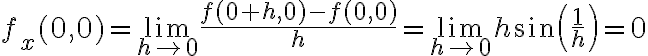Buenas, me podrían dar una mano con este ejercicio? no estoy logrando hacerlo, gracias
Ejercicio 3Segundo Parcial 2018 2do semestre
Número de respuestas: 5Re: Ejercicio 3Segundo Parcial 2018 2do semestre
Hola. Te recomiendo estudiar las derivadas parciales y las direccionales usando la definición, es decir, planteando los cocientes incrementales en  . Por ejemplo, la derivada parcial respecto a
. Por ejemplo, la derivada parcial respecto a  es:
es:
Si hacés lo mismo con la derivada parcial respecto a  te va a dar 1 y si planteás la derivada direccional respecto a una dirección cualquiera
te va a dar 1 y si planteás la derivada direccional respecto a una dirección cualquiera 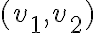 te da 0. Entonces,la función no puede ser diferenciable, porque si lo fuera la derivada direccional respecto
te da 0. Entonces,la función no puede ser diferenciable, porque si lo fuera la derivada direccional respecto 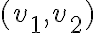 debería darte
debería darte 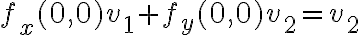 .
.
Saludos
Re: Ejercicio 3Segundo Parcial 2018 2do semestre
Acá entra la otra consulta, no entendí tu afirmación final que dice "...porque si lo fuera la derivada direccional respecto (v1,v2) debería darte fx(0,0).v1+fy(0,0).v2 = v2" ya que si la derivada según X, es 0 y la derivada según Y, es 1, eso te queda 0.v1+1.v2=v2 que es v2=v2 y si se cumpliría la diferenciabilidad según tu ultimo enunciado, si es que no lo entendí mal.
Desde ya muchas gracias
Saludos
Rodrigo
Re: Ejercicio 3Segundo Parcial 2018 2do semestre
 no es diferenciable en
no es diferenciable en  , pero existen la derivadas parciales en un entorno de
, pero existen la derivadas parciales en un entorno de  ". Es decir, está diciendo que las derivadas parciales existen para todos los puntos
". Es decir, está diciendo que las derivadas parciales existen para todos los puntos 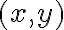 en un entorno de
en un entorno de  (y no solo en ese punto, como dice la afirmación (C)). Para ver que eso no es cierto, podés ver que en cualquier punto de la forma
(y no solo en ese punto, como dice la afirmación (C)). Para ver que eso no es cierto, podés ver que en cualquier punto de la forma 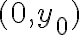 con
con 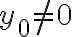 (es decir, cualquier punto en el eje
(es decir, cualquier punto en el eje  que no sea el origen) la derivada parcial según
que no sea el origen) la derivada parcial según  no existe. Para ver eso vas a tener que plantear el cociente incremental para un punto de la forma
no existe. Para ver eso vas a tener que plantear el cociente incremental para un punto de la forma 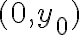 .
. es diferenciable en
es diferenciable en 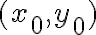 entonces la derivada direccional respecto a una dirección
entonces la derivada direccional respecto a una dirección 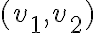 es
es 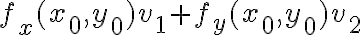 . En este caso, como me interesa lo que pasa en
. En este caso, como me interesa lo que pasa en  , lo que me dice ese teorema es que si fuese diferenciable en ese punto la derivada direccional debería dar
, lo que me dice ese teorema es que si fuese diferenciable en ese punto la derivada direccional debería dar 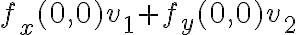 . Como para esta
. Como para esta  en particular
en particular  y
y 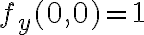 , esa cuenta da
, esa cuenta da 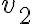 (eso es lo que puse a la derecha del igual, no quiere decir que para todas las funciones diferenciables esa cuenta tenga que dar
(eso es lo que puse a la derecha del igual, no quiere decir que para todas las funciones diferenciables esa cuenta tenga que dar 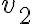 ). Sin embargo, como hice la cuenta a mano con el cociente incremental y la derivada direccional no me dio
). Sin embargo, como hice la cuenta a mano con el cociente incremental y la derivada direccional no me dio 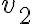 , puedo concluir que la función no puede ser diferenciable en el
, puedo concluir que la función no puede ser diferenciable en el  .
.Re: Ejercicio 3Segundo Parcial 2018 2do semestre
No logro entender porqué no existe la derivada parcial respecto a x en los puntos de la forma (0,yo).
Tampoco entendí porqué la afirmación C implica que existen las derivadas parciales para todos los puntos (x,y) si en realidad la afirmación dice que existen para "un" entorno de (0,0).
Saludos.
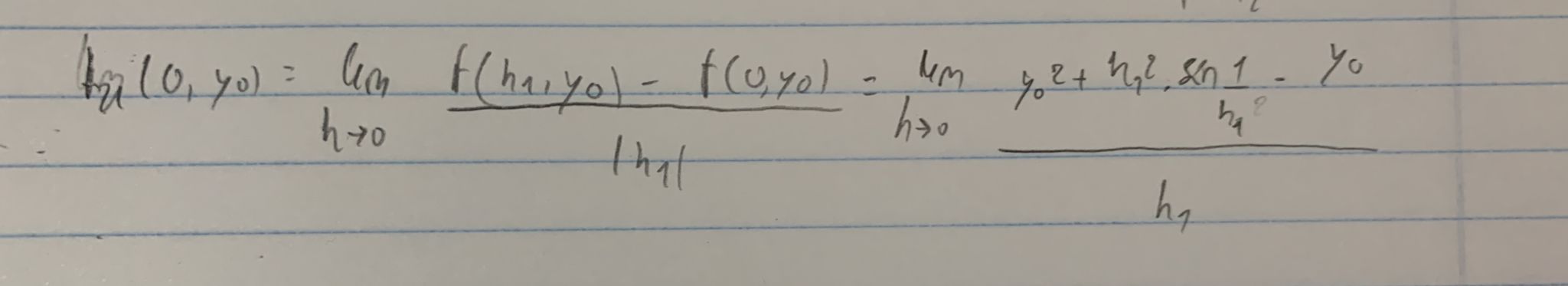
Re: Ejercicio 3Segundo Parcial 2018 2do semestre
Hola. La derivada parcial según  no existe en esos puntos porque ese último límite que planteaste da
no existe en esos puntos porque ese último límite que planteaste da 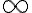 si
si 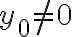 .
.
Sobre la otra pregunta: la afirmación (C) dice que existen todas las derivadas parciales en  . La (A) es la que habla de la existencia de las derivadas parciales en un entorno del
. La (A) es la que habla de la existencia de las derivadas parciales en un entorno del  . Cuando dice eso, quiere decir que existe UN entorno del
. Cuando dice eso, quiere decir que existe UN entorno del  tal que las derivadas parciales existen en todo punto de ese entorno. Formalmente, dice que existe un radio
tal que las derivadas parciales existen en todo punto de ese entorno. Formalmente, dice que existe un radio 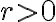 tal que para todo
tal que para todo 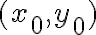 en la bola de centro
en la bola de centro  y radio
y radio  existen las derivadas parciales
existen las derivadas parciales  y
y 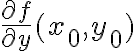 .
.
Saludos