Buenas, se me complica sacar el dominio, más que nada en la primera desigualdad. Y después de eso como pasarlo con el cambio a polares.
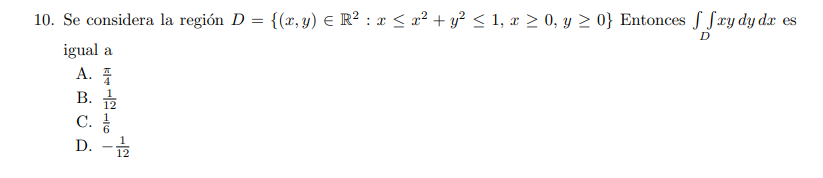
Buenas, se me complica sacar el dominio, más que nada en la primera desigualdad. Y después de eso como pasarlo con el cambio a polares.
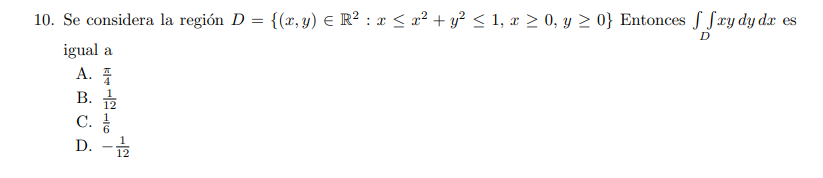
Buenas!
Para poder ver el dominio podemos tratar cada desigualdad por separado, es decir: 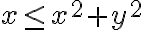 y
y 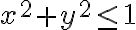
En el segundo caso tenemos el interior de un círculo de radio  mientras que en el primero también tenemos un círculo pero para verlo tenemos que hacer un par de cuentas:
mientras que en el primero también tenemos un círculo pero para verlo tenemos que hacer un par de cuentas:
Es decir, lo que buscamos es hacer aparecer binomios al cuadrado, ahora lo que tenemos es el exterior del círculo de centro 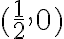 y radio
y radio 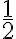 , es decir, con la desigualdad
, es decir, con la desigualdad 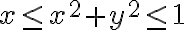 tenemos la siguiente figura:
tenemos la siguiente figura:
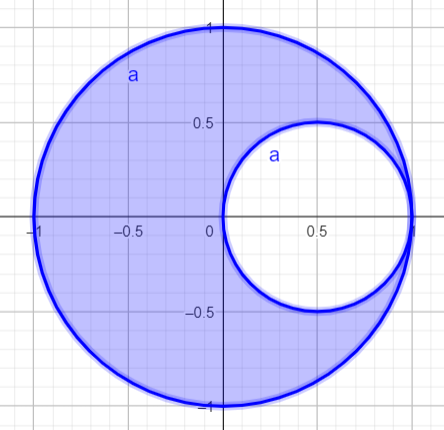
Además nos dicen 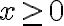 e
e 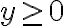 por lo que estaremos solo en el primer cuadrante.
por lo que estaremos solo en el primer cuadrante.
Ahora para pasar a polares volvemos a ver las desigualdades:
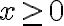 e
e 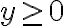 estas nos dan la información sobre
estas nos dan la información sobre  :
: ![\theta \in [0,\frac{\pi}{2}] \theta \in [0,\frac{\pi}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/f324d322baf7f8a896928fe79dc1ceb3.gif)
Como en polares 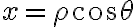 e
e 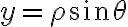 podemos sustituir este cambio de variable en
podemos sustituir este cambio de variable en 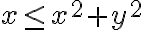 y
y 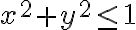 para ver entre qué extremos dejamos a
para ver entre qué extremos dejamos a 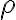 :
:
Por lo tanto:
Saludos!
Florencia