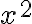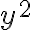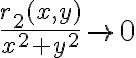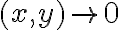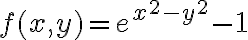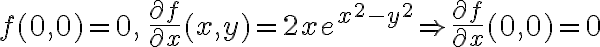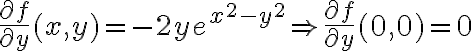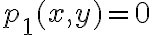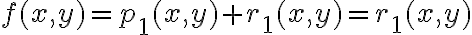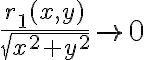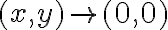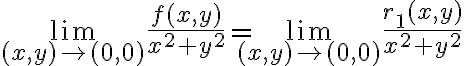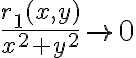Resto en Taylor

Resto en Taylor

de Pedro Manuel Carreras Salaberry -
Número de respuestas: 4

Hola tengo una duda de como usar el resto cuando usamos equivalentes en limites, ya que en este caso el resto seria de orden 1 pero a veces no esta dividido la norma, pero si dividido la norma tiende a 0, sin dividir también, no? pero en este ejemplo no se como ver que el resto de orden 1 tiende a 0: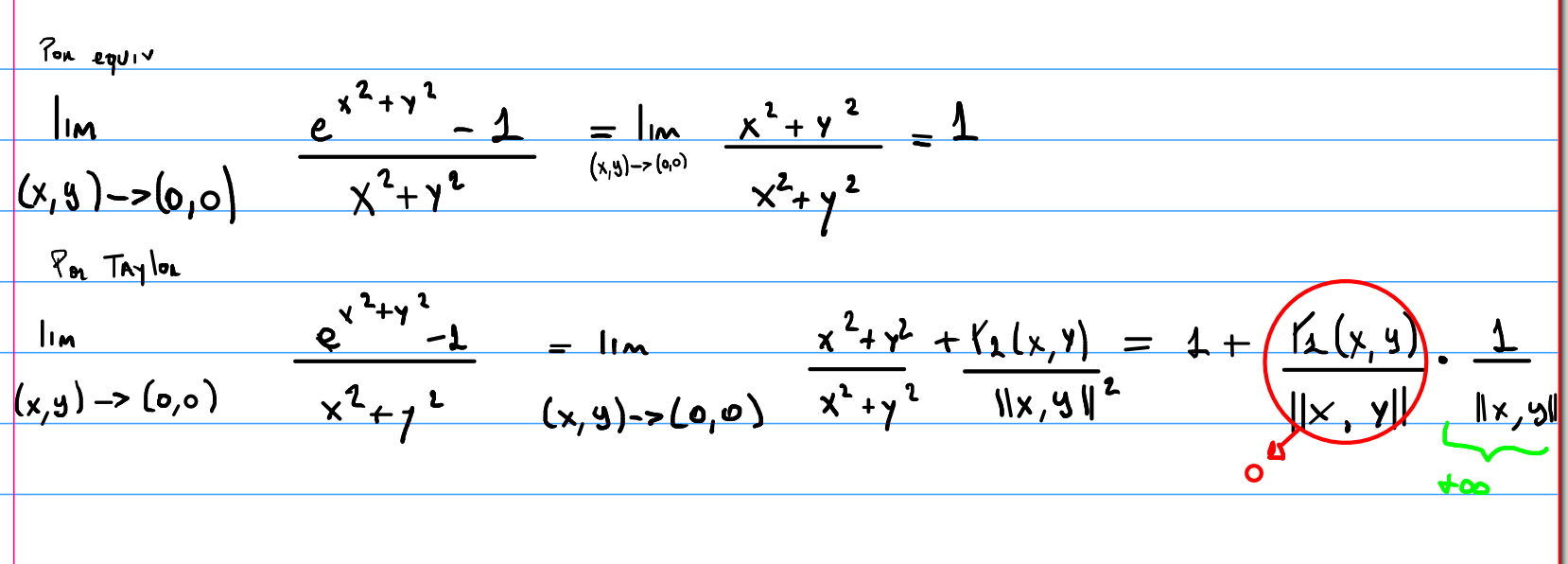 

Haciendo un desarrollo de orden 2 si puedo ver que tiende a 0 pero entonces como sabemos cuando podemos usar equivalentes?

En respuesta a Pedro Manuel Carreras Salaberry

Re: Resto en Taylor

de Bernardo Marenco -

Hola. En este caso estás haciendo un desarrollo de orden 2, no de orden 1 (fijate que los términos del desarrollo son x^2 e y^2). Por lo tanto, el resto cumple que \displaystyle \frac{r_2(x,y)}{x^2+y^2} \to 0 cuando (x,y) \to 0. Fijate que para que ese cociente tienda a 0 el numerador tiene que tender a 0 (y más rápido que el denominador).

Saludos
En respuesta a Bernardo Marenco

Re: Resto en Taylor

de Pedro Manuel Carreras Salaberry -
Bien entiendo, me equivoque al hacer el ejemplo, mi idea era que quedara un ejemplo donde en el numerador quedara un polinomio mas un resto de orden 1 y en el denominador la norma al cuadrado, entonces ahí podría simplemente "sacar" el resto ya que tiende a 0 o solo lo podemos "sacar" cuando esta dividido la norma?
En respuesta a Pedro Manuel Carreras Salaberry

Re: Resto en Taylor

de Bernardo Marenco -

No, en ese caso no podrías "sacar" el resto, porque lo único que sabés es que el resto de orden 1 tiende a 0 más rápido que \sqrt{x^2+y^2}. Eso no necesariamente implica que tienda a 0 más rápido que x^2+y^2, que es de un orden de magnitud más grande. Fijate en tu ejemplo: si llamás f(x,y)=e^{x^2-y^2}-1, entonces \displaystyle f(0,0)=0,\, \frac{\partial f}{\partial x}(x,y) = 2xe^{x^2-y^2}\Rightarrow \frac{\partial f}{\partial x}(0,0) = 0 y \displaystyle \frac{\partial f}{\partial y}(x,y) = -2ye^{x^2-y^2}\Rightarrow \frac{\partial f}{\partial y}(0,0) = 0. Entonces el polinomio de Taylor de orden 1 de f en (0,0) sería p_1(x,y) = 0, y por lo tanto f(x,y)=p_1(x,y) + r_1(x,y) = r_1(x,y), donde \frac{r_1(x,y)}{\sqrt{x^2+y^2}} \to 0 cuando (x,y) \to (0,0). Si sustituís esa igualdad en el límite, te queda:

\displaystyle \lim_{(x,y) \to (0,0)} \frac{f(x,y)}{x^2+y^2} = \lim_{(x,y) \to (0,0)} \frac{r_1(x,y)}{x^2+y^2}

Usando tu razonamiento, ese límite sería 0 porque el resto de orden 1 tiende a 0. Pero ya sabés que haciendo un Taylor de orden 2 ese límite da 1. De nuevo, el error está en asumir que \frac{r_1(x,y)}{x^2+y^2} \to 0, lo que no sabemos si es cierto (de hecho el razonamiento de arriba prueba que \frac{r_1(x,y)}{x^2+y^2} \to 1).

Saludos