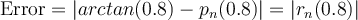Hola! Estuve intentando hacer este ejercicio haciendo Taylor en los ordenes que pedía, pero no llegue a ninguna solución. Como se resuelve?
En respuesta a Maria Sofia Camacho Lamboglia
Re: Ejercicio 1 (Ejercicios Opcionales)
de Bernardo Marenco -
Hola. El ejercicio es un ejercicio de Taylor en una variable. La idea es aproximar el valor que se pide por el que da el polinomio de Taylor en un punto cercano. Por ejemplo, para la parte a) podés calcular el polinomio de Taylor de arcotangente en 0 y tomar como aproximación cuánto vale ese polinomio en 0.8. Así, la diferencia entre la aproximación y el valor real es el resto en ese punto, ya que:
Usando la fórmula de Lagrange para el resto se puede acotar cuánto vale 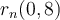 en función de
en función de  , y entonces podés elegir
, y entonces podés elegir  para que ese error sea más chico que lo que pide la letra.
para que ese error sea más chico que lo que pide la letra.
Saludos