Hola, estoy asustado porque me vienen saliendo bastante bien los ejercicios de Taylor en 2 variables, pero no he podido con ninguno de los 3 de la parte de "repaso". Estos límites son de dificultad considerablemente mayor en comparación con cualquiera de los que hayamos visto en CDI1V, pero luego de reiterados intentos no logro dar en la tecla. Temo estar perdiéndome de algo. Me quedan en general desarrollos super largos que terminan de la forma 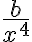 , dónde
, dónde  es una constante cualquiera, dando el límite:
es una constante cualquiera, dando el límite: 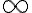 .
.
¿Alguna sugerencia?
Hola Diego. Capaz podés subir tu resolución de alguno de esos ejercicios para ver bien cuál está siendo el problema. Así en el aire es difícil de contestarte. Lo que se me ocurre es que estés planteando el Taylor hasta un orden menor al necesario para calcular el límite y que te estés olvidando del resto. Pero si podés subí una foto con lo que hayas hecho así lo vemos bien.
Saludos
Estimado Bernardo, adjunto fotos de los ejercicios 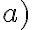 y
y 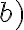 . Pido disculpas por los tachones, es que cuando un ejercicio no me salió lo tacho para no creer luego que es un buen ejemplo de resolución.
. Pido disculpas por los tachones, es que cuando un ejercicio no me salió lo tacho para no creer luego que es un buen ejemplo de resolución.
1-a) Este lo intenté de 3 maneras:
1-Desarrollando 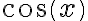 hasta grado 4 y luego sustituyendo
hasta grado 4 y luego sustituyendo 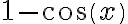 por
por 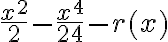 . En otro intento que no muestro expreso el resto como
. En otro intento que no muestro expreso el resto como 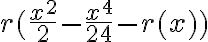 , que no sé si tiene sentido alguno. (1ra foto)
, que no sé si tiene sentido alguno. (1ra foto)
2-Desarrollando 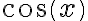 hasta grado 4 y luego sustituyendo
hasta grado 4 y luego sustituyendo  por
por 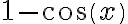 . (2da foto)
. (2da foto)
3-Desarrollando 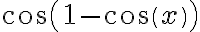 hasta grado 2 porque luego vi que no tenía sentido, ya que me quedaban expresiones multiplicadas por
hasta grado 2 porque luego vi que no tenía sentido, ya que me quedaban expresiones multiplicadas por 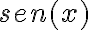 y/o por
y/o por 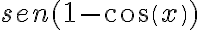 y al evaluar en
y al evaluar en  no obtenía nada.
no obtenía nada.
1-b) Desarrollo las 4 funciones hasta grado 3, pero luego (2da foto del Ej.b) no sé como seguir. Probé luego desarrollar unas y no otras, pero no doy en la tecla. (3er y 4ta foto)
1-c) Desarrollo 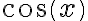 hasta grado 4. Multiplico y divido por
hasta grado 4. Multiplico y divido por 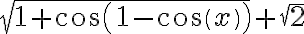 para "deshacerme" de las raíces. Luego sustituyo como en la manera 2 de la parte
para "deshacerme" de las raíces. Luego sustituyo como en la manera 2 de la parte 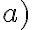 .
.
(Intenté también desarrollar 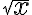 pero a las derivadas no se las puede evaluar en
pero a las derivadas no se las puede evaluar en  )
)
Espero se entienda.
Saludos!



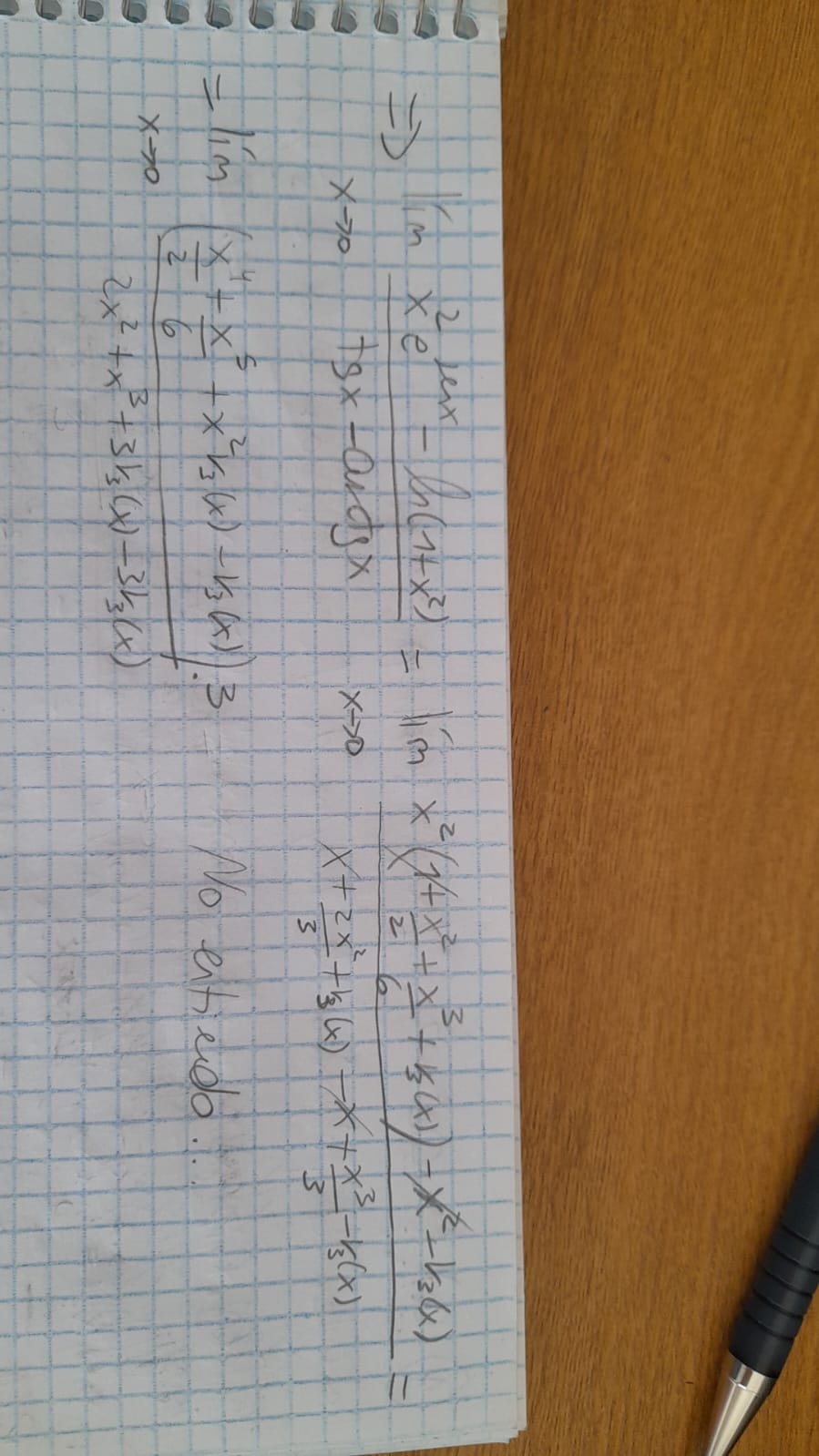
Hola Diego. Un tema que veo que se repite en tus resoluciones es que hallás el polinomio de Taylor de una función y luego lo componés/multiplicás con el de otra para hallar el polinomio que buscás. Por ejemplo, en el ejercicio 1a), hallás el Taylor de coseno y después lo componés con el mismo polinomio. Hay que tener cuidado con eso, porque no necesariamente te lleva a buen puerto. Por ejemplo, como 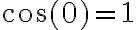 , si busco el Taylor de
, si busco el Taylor de 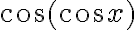 en
en 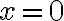 , el coseno de afuera "está evaluado" en
, el coseno de afuera "está evaluado" en  . O sea que si querés usar el camino de la composición, tendrías que componer el el Taylor de coseno en 0 con el Taylor de coseno en 1. Lo que te recomiendo que hagas (que entiendo que fue tu 3er intento de resolución del ejercicio) es tomar como función a
. O sea que si querés usar el camino de la composición, tendrías que componer el el Taylor de coseno en 0 con el Taylor de coseno en 1. Lo que te recomiendo que hagas (que entiendo que fue tu 3er intento de resolución del ejercicio) es tomar como función a 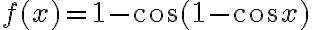 y le halles el Taylor a esa función. Es decir, la derives tantas veces como el orden del polinomio que quieras calcular y vayas evaluando en el punto en el que quieras calcular el polinomio (
y le halles el Taylor a esa función. Es decir, la derives tantas veces como el orden del polinomio que quieras calcular y vayas evaluando en el punto en el que quieras calcular el polinomio (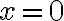 en ese ejercicio). Creo que tu problema con esa parte fue que solo fuiste hasta grado 2, cuando para poder hallar el límite tenés que hacer el Taylor de orden 4. Ojo con esta afirmación: "Desarrollando
en ese ejercicio). Creo que tu problema con esa parte fue que solo fuiste hasta grado 2, cuando para poder hallar el límite tenés que hacer el Taylor de orden 4. Ojo con esta afirmación: "Desarrollando 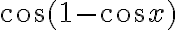 hasta grado 2 porque luego vi que no tenía sentido, ya que me quedaban expresiones multiplicadas por
hasta grado 2 porque luego vi que no tenía sentido, ya que me quedaban expresiones multiplicadas por 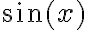 y/o por
y/o por 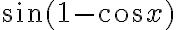 y al evaluar en 0 no obtenía nada". Eso lo único que te dice es que el Taylor de orden 2 de
y al evaluar en 0 no obtenía nada". Eso lo único que te dice es que el Taylor de orden 2 de 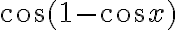 en 0 es
en 0 es 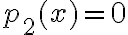 . No hay contradicción en eso; a pesar de su nombre el polinomio de Taylor de orden
. No hay contradicción en eso; a pesar de su nombre el polinomio de Taylor de orden  es un polinomio de grado menor o igual a
es un polinomio de grado menor o igual a  (puede tranquilamente ser menor).
(puede tranquilamente ser menor).
En el 1b), de nuevo, en vez de hacer el Taylor de 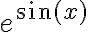 y luego multiplicarlo por
y luego multiplicarlo por 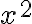 , te recomiendo hallar directamente el Taylor de
, te recomiendo hallar directamente el Taylor de 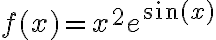 hasta el orden que necesites. El otro camino no está mal, pero es más fácil equivocarte en algún paso.
hasta el orden que necesites. El otro camino no está mal, pero es más fácil equivocarte en algún paso.
Fijate si esto te ayuda. Saludos
Saludos!
