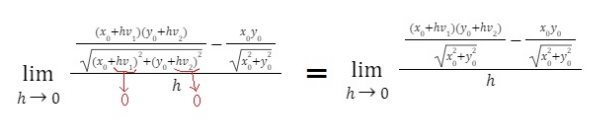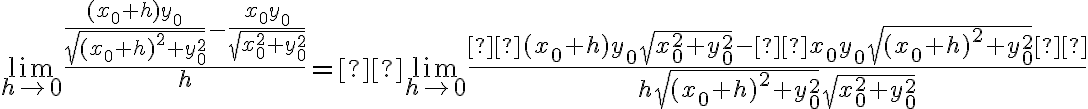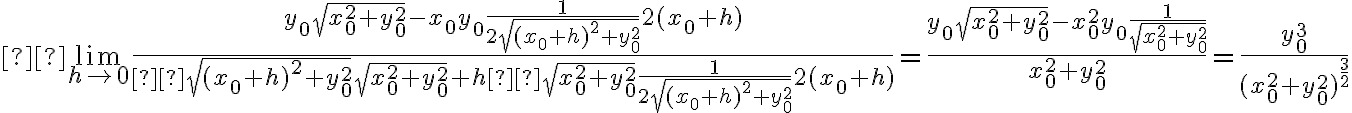ej 4.a

ej 4.a

de Camilo Fernandez Lapettina -
Número de respuestas: 5

hola buenas, tenia una duda, en el ejercicio 4.a, calcule las derivadas parciales como las calculamos normalmente, y luego fui a calcular las derivadas direccionales para verificar su existencia, y a pesar de que esto ultimo me dio bien, los dos resultados no son coherentes entre si, y no veo donde está el error

la función era:

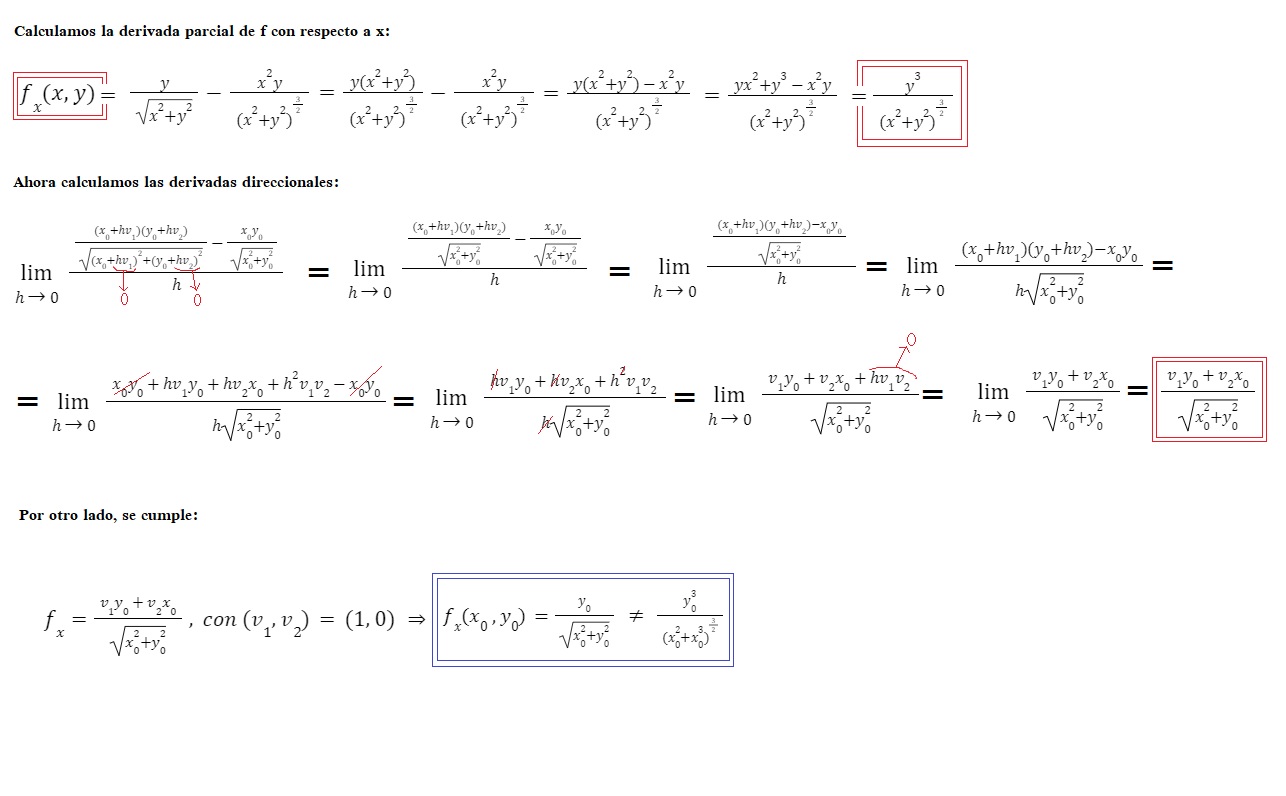
 qu2XyIBRp6XOP4Vkin6Oqbt8nKeDfCIsGKDTnTTp9eYp9FNvQ32zbmp3TSTH0K0ipVDatLNGJBkXSA_RlU1CwUPn2U9hhVuS7KwkLplgmKKICCPJneZ9IOgkEgHwPAVoYz1bwoET0IYWHK7OGMzclnXns-SIKEd1BAlOIwSXiC2YmEqpBbaPoLXsCg


y esto fue lo que yo hice:


En respuesta a Camilo Fernandez Lapettina

Re: ej 4.a

de Camilo Fernandez Lapettina -
buenas, ha pasado una semana desde que hice la pregunta y no tengo respuesta
En respuesta a Camilo Fernandez Lapettina

Re: ej 4.a

de Florencia Uslenghi -
Hola Camilo!
El error está en el cálculo del límite de la derivada direccional, en el segundo paso, es decir, en este paso:
limite derivada direccional
Lo correcto sería hacer denominador común y seguir operando, muestro el procedimiento ya tomando (v_1,v_2)=(1,0):
\lim_{h \rightarrow 0} \frac{ \frac{ (x_0+h)y_0 }{ \sqrt{ (x_0+h)^2 +y_0^2 } } - \frac{x_0y_0}{\sqrt{ x_0^2 +y_0^2 }} }{ h } = \lim_{h \rightarrow 0} \frac{ (x_0+h)y_0\sqrt{ x_0^2 +y_0^2 } -  x_0y_0\sqrt{ (x_0+h)^2 +y_0^2 } }{ h \sqrt{ (x_0+h)^2 +y_0^2 }\sqrt{ x_0^2 +y_0^2 }}
Ahora tenemos una indeterminación donde podemos aplicar L'Hopital:
 \lim_{h \rightarrow 0} \frac{ y_0 \sqrt{ x_0^2 +y_0^2 } - x_0y_0\frac{1}{2\sqrt{ (x_0+h)^2 +y_0^2 }} 2(x_0 + h) }{ \sqrt{ (x_0+h)^2 +y_0^2 }\sqrt{ x_0^2 +y_0^2 } + h \sqrt{ x_0^2 +y_0^2 } \frac{1}{2\sqrt{ (x_0+h)^2 +y_0^2 }} 2(x_0 + h) } = \frac{ y_0 \sqrt{ x_0^2 +y_0^2 } - x_0^2y_0 \frac{1}{\sqrt{ x_0^2 +y_0^2 }} }{x_0^2+y_0^2} = \frac{y_0^3}{(x_0^2+y_0^2)^{\frac{3}{2}}}
Por lo que llegamos al mismo valor, para la forma general es el mismo procedimiento pero tiene bastante más cuentas. 
Cualquier cosa a las órdenes :)
Saludos,
Florencia
En respuesta a Florencia Uslenghi

Re: ej 4.a

de Camilo Fernandez Lapettina -
por que es que no se puede hacer eso?, como hv1 y hv2 tienden a 0, en el limite no tendrían efecto, ese fue mi razonamiento
En respuesta a Camilo Fernandez Lapettina

Re: ej 4.a

de Florencia Uslenghi -
Porque ahí tenés una indeterminación, cuando haces tender esos términos a cero perdes información que después es importante. Si pudieras considerar esos términos como cero a esa altura también deberías poder considerarlos cero en el numerador de ese término.