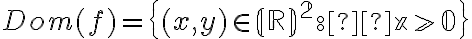Hola tengo una duda, en las soluciones de este ejercicio está que el dominio de la función no es todo R^2 pero no entiendo por qué ya que no presenta ningún problema de existencia cuál sería el argumento para restringir el dominio?
Buenos días!
En este caso estábamos buscando el dominio de la función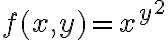 por lo que podemos hacer lo que sugiere la solución y reescribir la exponencial como:
por lo que podemos hacer lo que sugiere la solución y reescribir la exponencial como: 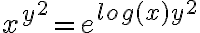 Así podemos ver que no hay ninguna restricción para
Así podemos ver que no hay ninguna restricción para  , sin embargo
, sin embargo 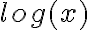 sí nos impone condiciones ya que
sí nos impone condiciones ya que  se encuentra dentro del logaritmo y por lo tanto para que esté definido debe cumplirse
se encuentra dentro del logaritmo y por lo tanto para que esté definido debe cumplirse 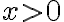 . De esta forma llegamos a que el dominio es todo el plano derecho:
. De esta forma llegamos a que el dominio es todo el plano derecho:
En este caso estábamos buscando el dominio de la función
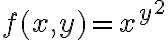 por lo que podemos hacer lo que sugiere la solución y reescribir la exponencial como:
por lo que podemos hacer lo que sugiere la solución y reescribir la exponencial como: 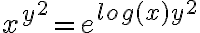 Así podemos ver que no hay ninguna restricción para
Así podemos ver que no hay ninguna restricción para  , sin embargo
, sin embargo 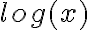 sí nos impone condiciones ya que
sí nos impone condiciones ya que  se encuentra dentro del logaritmo y por lo tanto para que esté definido debe cumplirse
se encuentra dentro del logaritmo y por lo tanto para que esté definido debe cumplirse 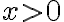 . De esta forma llegamos a que el dominio es todo el plano derecho:
. De esta forma llegamos a que el dominio es todo el plano derecho: Saludos!
Florencia
Hola entiendo cómo queda el dominio una vez pasado a la forma e^b.log(x), pero en esta forma no podemos obtener el -1 y en la forma x^(y^2) si y mientras y=√(número impar) y a negativo nos devolvería un negativo siempre, entonces entiendo que los dominios de ambas funciones no son iguales no?
Hola Pedro,
Es una buena pregunta sí. Comenzemos tomando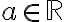 negativo. Como vos decís no hay problema al definir
negativo. Como vos decís no hay problema al definir 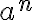 con
con 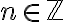 , de hecho, podríamos llegar a definir
, de hecho, podríamos llegar a definir 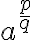 con
con 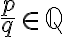 cuando
cuando  es impar, porque todo número real tienen una única raíz
es impar, porque todo número real tienen una única raíz  -ésima real. El problema lo vamos a tener cuando queremos definir
-ésima real. El problema lo vamos a tener cuando queremos definir 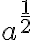 , o de hecho, cuando queramos elevar
, o de hecho, cuando queramos elevar  por cualquier racional cuyo denominador sea par. La solución es restringirnos a tomar los reales positivos en la base como comentó Florencia.
por cualquier racional cuyo denominador sea par. La solución es restringirnos a tomar los reales positivos en la base como comentó Florencia.
Hay otro encare donde sí podemos definir la función con negativos, que es extendiendo la función a los complejos y ahí podemos elegir una semirrecta cualquiera desde el origen que quede fuera del dominio de definición, pero para esto es necesario conocimientos de un curso de análisis complejo.
negativos, que es extendiendo la función a los complejos y ahí podemos elegir una semirrecta cualquiera desde el origen que quede fuera del dominio de definición, pero para esto es necesario conocimientos de un curso de análisis complejo.
Saludos,
Leandro
Es una buena pregunta sí. Comenzemos tomando
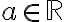 negativo. Como vos decís no hay problema al definir
negativo. Como vos decís no hay problema al definir 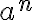 con
con 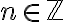 , de hecho, podríamos llegar a definir
, de hecho, podríamos llegar a definir 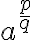 con
con 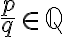 cuando
cuando  es impar, porque todo número real tienen una única raíz
es impar, porque todo número real tienen una única raíz  -ésima real. El problema lo vamos a tener cuando queremos definir
-ésima real. El problema lo vamos a tener cuando queremos definir 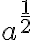 , o de hecho, cuando queramos elevar
, o de hecho, cuando queramos elevar  por cualquier racional cuyo denominador sea par. La solución es restringirnos a tomar los reales positivos en la base como comentó Florencia.
por cualquier racional cuyo denominador sea par. La solución es restringirnos a tomar los reales positivos en la base como comentó Florencia.Hay otro encare donde sí podemos definir la función con
 negativos, que es extendiendo la función a los complejos y ahí podemos elegir una semirrecta cualquiera desde el origen que quede fuera del dominio de definición, pero para esto es necesario conocimientos de un curso de análisis complejo.
negativos, que es extendiendo la función a los complejos y ahí podemos elegir una semirrecta cualquiera desde el origen que quede fuera del dominio de definición, pero para esto es necesario conocimientos de un curso de análisis complejo.Saludos,
Leandro
Se entendió, muchas gracias