Hola!! Yo intente hacer este límite con direccionales, usando la recta general y=mx. Por lo que entendí, si llego a un limite que no depende de m, existe y es ese, pero si depende de m, no existe. Por lo tanto, aca supondría que no existe. No entiendo bien qué esta mal en el razonamiento anterior, pq la respuestas dice que da 3/2, como si impusiera m=1. Desde ya gracias!!
Yo tengo la misma duda. Me parece que al reemplazar Y por una función (en este caso una recta), ésta debe pasar por el punto del limite. O sea, y = mx no es correcto, porque no estás pasando por 0 sino por 1, en su lugar sería y = mx + n. El problema es que igualmente el limite sigue dependiendo de m, si no lo calculé mal. xD
Hola. Lo que dice Marcos es verdad: la recta tiene que pasar por el punto, así que en este caso para que pase por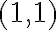 
deberían tomar una recta de la forma 
.
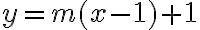Un detalle sobre esta afirmación: "si llego a un limite que no depende de m, existe y es ese, pero si depende de m, no existe". Es cierto que si el resultado del límite direccional depende de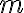 
entonces el límite no existe. Sin embargo, los límites por rectas pueden no depender de 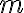y que igual el límite no exista. Un ejemplo de eso es el ejercicio 4.c), parte iii) o el ejercicio 9 del práctico 7. El ejemplo 5.12 de la página 84 de las notas del curso también muestra esto, y copio algo que se dice ahí: "Tenemos entonces que los límites direccionales, por cualquier recta, son cero. Sin embargo, esto no alcanza para concluir que existe el límite. Lo único que podemos afirmar es que, si el límite existe, debe ser cero". En ese ejemplo se muestra cómo acercándose al punto por otras trayectorias es posible probar que el límite no existe. Y concluye con una observación que me parece muy útil: "Es importante recordar que los límites direccionales no permiten garantizar la existencia del límite. Son útiles para hallar un candidato a límite, o para demostrar que el límite no existe".
Saludos
Entonces en este ejercicio que piden calcular el limite, habria que usar polares? Tengo entendido que por polares si se puede garantizar que el limite exista y sea ese, no?
Hola. En ese ejercicio creo que lo más fácil es escribir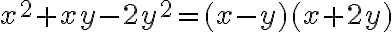 
y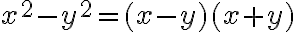 
y cancelar los 
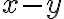del numerador y del denominador.
Sobre lo de polares, el ejercicio 4 muestra que si el límite por polares existe eso no necesariamente implica que el límite original existe. La parte 4e) muestra que eso vale si podés escribir el límite con polares como algo que tiende a 0 con 
por algo acotado en 
. En ese caso podés garantizar que el límite existe y es 0.
Saludos