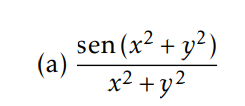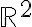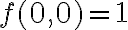Buenas tardes, no logro entender porque esta función es continua en todo el plano, según dice la respuesta. Si bien el limite tendiendo x,y a (0,0) es 1, el valor funcional en (0,0) no existe entonces no dejaría de ser continua?
Soy consciente del hecho de que si es continua en su dominio, es decir en donde esta bien definida. Pero el ejercicio trata de extenderlas en todo el plano R°2, por lo que el punto (0,0) cae dentro y eso me genero confusión, gracias.