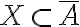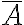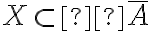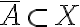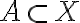Ejercicio 6) d)

Ejercicio 6) d)

de Diego Subeldia Loureiro -
Número de respuestas: 2

Buenas noches, les agradezco si pueden ayudarme a demostrar que la clausura de A es la intersección de todos los conjuntos cerrados que contienen a A.
Pude demostrar que es cerrado, pero no me doy cuenta de como jugar con esas ideas para probar también eso otro.

Saludos!
En respuesta a Diego Subeldia Loureiro

Re: Ejercicio 6) d)

de Leandro Bentancur -
Hola Diego,

Para probar que dos conjuntos son iguales hay que probar una doble inclusión. Llamemos X a la intersección de todos los conjuntos cerrados que contienen a A

Por un lado queremos ver que X \subset \overline{A}. Como \overline{A} es cerrado, tenemos que X \subset \overline{A} porque justamente X es la intersección de \overline{A} con más conjuntos.

La otra inclusión es \overline{A} \subset X. Sabemos que A \subset X. Qué pasa con esta inclusión si clausuramos ambos?

Cualquier cosa volvé a comentar por acá nomás.

Saludos,
Leandro