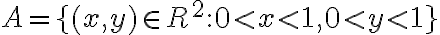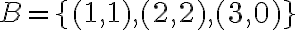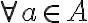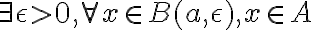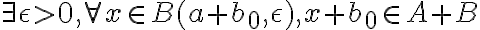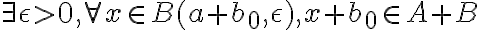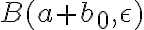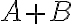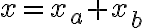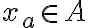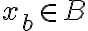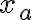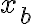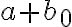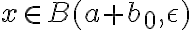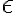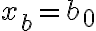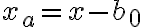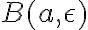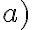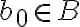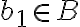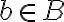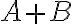CDIVV-2S: Ejerció 5.a

Buenas noches,

Estuve pensando con un compañero un rato este ejercicio. Creo que llegamos a una demostración, pero no se si es valida. ¿Podrían mírala y comentarme que les parece? Y en caso de que haya errores, como corregirlos o por donde comenzar de nuevo.

Sabemos que A es abierto y que se define a 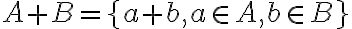$A+B = \lbrace{a+b, a \in A, b \in B }\rbrace$

Para fijar un poco de conceptos y ver por donde podíamos atacar esto pensamos en un pequeño ejemplo:

$A = \lbrace{(x,y) \in R^2 : 0 < x < 1 , 0 < y < 1 }\rbrace$

$B = \lbrace{(1,1), (2,2) , (3,0)}\rbrace$

Cuando buscamos los elementos de A+B nos dimos cuenta que tiene sentido crear 3 nuevos cuadrados, al primero desplazarlo 1 a la izquierda y uno hacia arriba (1,1). Para el segundo dos hacia arriba y dos a la izquierda, y para el ultimo solamente 3 a la izquierda.

Por lo tanto, sabemos que al ser A abierto, no deja de serlo por ser duplicado y trasladado, por lo tanto, podríamos trasladar la bola generada por cada 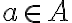$a \in A$ también.

Osea, un intento de formalizar esta idea podría ser que:

$\forall a \in A$ se cumple que $\exists \epsilon > 0 , \forall x \in B(a, \epsilon), x \in A$

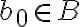Sea $b_0 \in B$ podemos sumarle a cada a 'a' y a cada x un b0. Por lo tanto nos quedaría algo así:

$\exists \epsilon > 0 , \forall x \in B(a+b_0, \epsilon), x + b_0 \in A + B$ (usando el mismo epison)

Entonces nos damos cuenta que 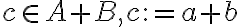$c \in A+B, c := a+b$ es interno. Si esto lo repetimos para cada todas las 'a' del conjunto A formamos un de los cuadrados duplicados, los cuales probamos (o al menos intentamos) que todos son internos. SI esto los repetimos con el resto de la b pertenecientes a B formamos todos los cuadrados duplicados, los cuales también todos sus puntos son internos de A+B.

Por lo tanto como todos los puntos de A+B son internos (ya que recorrimos ambos conjuntos) nos queda que A+B es abierto.

Concluyendo la demostración

Si me puede ayudar a mejorarlo o corregirlo agradezco

Saludos

Daniel

Re: Ejerció 5.a

de Veronica Rumbo - miércoles, 30 de septiembre de 2020, 11:22

Está muy bien la idea. Como sugerencia para mejorar la escritura, quizás probar más explícitamente la línea donde dicen

$\exists \epsilon > 0 , \forall x \in B(a+b_0, \epsilon), x + b_0 \in A + B$

Insisto, la idea está perfecta. Sólo para explicitar por qué es cierta esa afirmación: igual que al principio, estaría bueno constatar que dado un $x$ arbitrario en $B(a+b_0, \epsilon)$ , dicho punto efectivamente pertence a $A + B$ . Para ello, aprovechan la elección del epsilon que convenientemente hicieron, escribiendo $x = x_a + x_b$ con $x_a \in A$ y $x_b \in B$ . Hay que encontrar $x_a$ y $x_b$ (lo cual acompañado del dibujo correspondiente es mucho más ameno. Igual creo que ya tienen clarísima cuál es la construcción). La idea es que el punto $x$ es el trasladado de otro valor "igual ubicado" en la otra bola (la que estaba contenida en $A$ ).

En resumen, ustedes parten de un punto genérico en $A + B$ , que escribieron como $a + b_0$ . luego toman $x \in B(a+b_0, \epsilon)$ con $\epsilon$ elegido como ya dijeron y quieren escribir $x = x_a + x_b$ . Para ello, pueden tomar $x_b = b_0$ (que trivialmente pertenece a $B$ , y en consecuencia $x_a = x - b_0$ .

Lo que estaría faltando es ver que dicho

$x_a$ pertenece a

$A$ , para lo cual sugiero probar que, más aún, pertence a

$B(a, \epsilon)$ .

Viene bien encaminado, si se animan a escribir eso un poco mejor y compartirlo por acá, genial. Es una buena forma de ir agarrandole la mano al tema de la escritura de demostraciones (si les resulta tedioso usar latex para todo también pueden subir una hoja escaneada o una foto razonablemente legible).

Saludos.

Re: Ejerció 5.a

de Fabrizio Raffaelli Nabon - jueves, 1 de octubre de 2020, 18:41

Buenas. Creo que la parte a la pude probar bien con la explicación, pero tengo dudas con la parte b, a que se refiere con que se puede decir. Osea, es claro, me parece, que no se puede afirmar que A + B es cerrado pues en la parte a no se pone ninguna restricción a B, es decir B podría ser abierto, cerrado o ninguna que el resultado es el mismo. Pero no se si están buscando sacar alguna otra propiedad que no sea ser cerrado o abierto. No se algo con la frontera por ejemplo.

Re: Ejerció 5.a

de Veronica Rumbo - jueves, 1 de octubre de 2020, 23:40

Está bien tu intuición. La idea de la parte b es que constaten que, a diferencia de la parte anterior, con saber que $A$ es cerrado no basta para decir nada. La idea es que noten eso y lo prueben.

¿A qué me refiero con probarlo? A dar ejemplos de conjuntos $A$ y $B$ con $A$ cerrado, en los que el conjunto suma sea cerrado en un caso, no cerrado en otro. A modo de corroboración de que no se puede afirmar nada a priori sobre $A + B$

Re: Ejerció 5.a

de Diego Subeldia Loureiro - domingo, 9 de octubre de 2022, 19:11

Estimados, aprovecho a sumarme a la consulta.

Razoné la parte

$a)$ de la misma forma que los compañeros, y terminé aplicando lo mismo para la parte

$b)$ , es decir, que el conjunto

$A$ lo estoy trasladando según un vector

$b_{0} \in B$ , luego según otro

$b_{1} \in B$ , así con todos los

$b \in B$ , hasta que

$A+B$ es el resultado de la unión de todas esas traslaciones. En mi cabeza, el mencionado

$A+B$ final sería un conjunto cerrado o más de uno aislados pero cerrados.

Sin embargo, viendo la solución del práctico veo que no es así. Puedo entender el ejemplo que se muestra y por qué entonces el conjunto no es cerrado (no contiene al punto de acumulación 0), pero no sé qué parte de mi razonamiento está mal o qué posibilidades estoy dejando afuera y por eso no llegué a una contradicción.

Saludos y gracias.