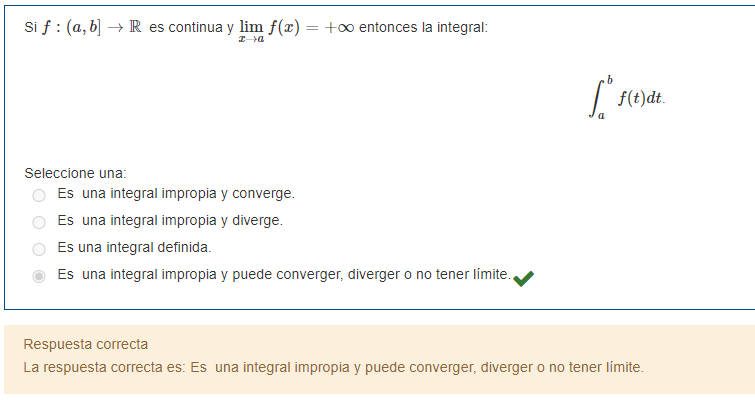
Hola, para esta funcion tenemos como ejemplos a f : (0, 1] en R / f(x) = 1/x y f(x) = 1/raiz de x. Como ejemplos de funciones que divergen y convergen. ¿Pero no debería ser imposible que no exista el limite? Es decir, si el limite cuando x tiende a (a) es infinito entonces existe delta tal que f(a, a+delta) es positivo. entonces separamos la integral en dos (a,a+delta] y [a+delta, b] donde la segunda no es impropia y la primera es toda positiva, por lo que al hacer el limite de la integral desde x hasta a+delta, donde x tiende a (a). Este limite tiene que existir porque a medida que x tiende a (a) solo estamos sumando más área, no puede oscilar por ser monótona.