Hola. En esa parte de la solución se está mirando a qué es equivalente el integrando cuando 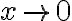 . Fijate que cuando
. Fijate que cuando  tiende a
tiende a  ,
, 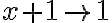 y por lo tanto
y por lo tanto 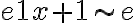 . Para el denominador, se me ocurren dos caminos para verlo:
. Para el denominador, se me ocurren dos caminos para verlo:
- Si llamamos
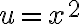 , entonces el denominador es
, entonces el denominador es 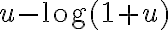 , que como función de
, que como función de  es equivalente a
es equivalente a 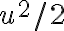 (eso lo podés ver haciendo un Taylor de orden 2 a
(eso lo podés ver haciendo un Taylor de orden 2 a 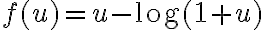 alrededor de
alrededor de 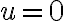 ). Entonces, deshaciendo el cambio de variable tenemos que
). Entonces, deshaciendo el cambio de variable tenemos que 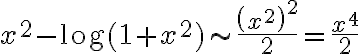 . En la solución hay un error en el denominador: hay un 4 en vez de un 2
(elevan todo el
. En la solución hay un error en el denominador: hay un 4 en vez de un 2
(elevan todo el 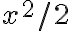 al cuadrado). Igual una diferencia en esa
constante no cambia la convergencia de la impropia.
al cuadrado). Igual una diferencia en esa
constante no cambia la convergencia de la impropia. - Podés llamar directamente
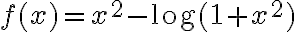 y hacer un Taylor de orden 4 de
y hacer un Taylor de orden 4 de  en 0 para ver que
en 0 para ver que 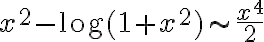
Saludos
