Foro de Ejercicios fuera de los Prácticos

Buenas!

La primera serie la podés sacar por comparación, viendo que 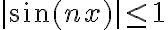$|\sin(nx)| \leq 1$ tenemos que 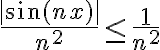$\frac{|\sin(nx)|}{n^2} \leq \frac{1}{n^2}$ como sabemos que $\sum_{n=1}^{\infty} \frac{1}{n^2} \ \mathbb{C}$ entonces  $\sum_{n=1}^{\infty}  \frac{|\sin(nx)|}{n^2} \  \mathbb{C}$

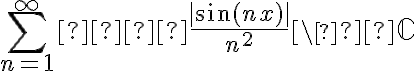
Pasamos a la segunda, cuando tengas dudas de cómo encarar siempre está bueno verificar que los términos que sumas en el infinito se hacen 0, ya que si 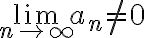$\lim_{n \rightarrow \infty} a_n \neq 0$ la serie diverge. En este caso:

$\lim_{n \rightarrow \infty } \frac{ \log{(n)} }{ \sqrt [n] { n+1 } } =  \lim_{n \rightarrow \infty }  (n+1)^{-\frac{1}{n}} \log{(n)}$

Reescribiéndolo de esta forma podemos ver que 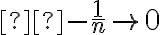$-\frac{1}{n} \rightarrow 0$ por lo que 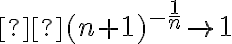$(n+1)^{-\frac{1}{n}} \rightarrow 1$ cuando 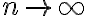$n \rightarrow \infty$ y por otro lado 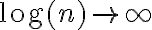$\log{(n)} \rightarrow \infty$ por lo que todo el límite anterior tiende a infinito, como es distinto de cero la serie diverge.

Saludos!

Florencia