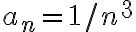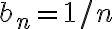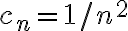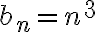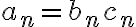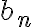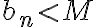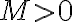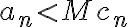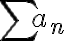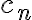Buenas, estuvimos discutiendo con un par de compañeros este ejercicio pero nos costó llegar a algunos resultados.

Como se puede ver ambos ejercicios son muy parecidos, solo varían en sí bn esta acotada o no, pero esto es suficiente para cambiar algunos resultados. Por eso decidimos analizar ambos casos a la par. En ambos ejercicios como la serie de cn converge entonces concluimos que cn tiende a cero y partimos de esto para pensar varias cosas.
Nuestro problema se dio en las oraciones 2 y 3 de ambos ejercicios. Pero quisiera contar como pensamos el 1 ya q capaz arrastramos algún razonamiento a las otras oraciones.
●En la oración 1 del ejercicio (1) supusimos q bn no puede tender a infinito ( puede tender a cero o a una constante) pero como también cn tiende a cero. Concluimos q la única posibilidad era q bn tendiera a una constante y an a cero y por esto bn Diverge.
●En la oración 1 del ejercicio (2) simple lo pensamos con ordenes, donde podemos tener dos sucesiones q tienden a infinito y el resultado del límite ser cero. Por eso también concluimos que bn Diverge.
■En la oración 2 del ejercicio ( 2) pensamos aplicar límites de ambos lados y operar de modo que quedara lo siguiente: Lim cn.bn=lim an
De modo que en este caso si bn no está acotada el limite de an puede no ser cero y por lo tanto diverger.
■Sin embargo en la oración 2 del ej (1) al aplicar el mismo razonamiento tenemos que acotado por cero da cero. Pero esto no es suficiente para concluir nada.
En las oraciones 3 no supimos como utilizar el resultado de que la serie de cero o no.
Agradezco si nos pueden guiar ya que llevamos un rato ya discutiendo este ejercicio y nos gustaría entenderlo por completo.