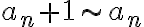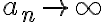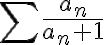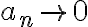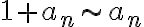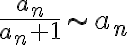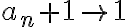Consulta cuestionario de series

Consulta cuestionario de series

de Valentina Gisel Tejera Luzardo -
Número de respuestas: 3
Buenas, quisiera consultar sobre este ejercicio.

En primer lugar hice  este razonamiento an/an+1 es equivalente a an/an y tener una sumatoria con este termino general implica que estoy sumando infinitas veces 1 y eso diverge, pero entonces an/an +1 diverge? Claramente este razonamiento no es correcto por q la letra lo aclara, pero quisiera saber q esta mal en el mismo. Por otro lado quisiera saber como resolver el ejercicio en si, trate de usar equivalentes pero llegue a desigualdades que no me dan nada de información. Tambien se me ocurrió usar el contrareciproco suponiendo que la sumatoria de an diverge, pero quede trancada en ello también. En fin, quisiera saber si pueden guiarme, muchisimas gracias.

Ejercicio

En respuesta a Valentina Gisel Tejera Luzardo

Re: Consulta cuestionario de series

de Bernardo Marenco -

Hola. Lo que no es correcto del razonamiento que estás haciendo es que estás diciendo que a_n +1 \sim a_n, pero eso vale si a_n \to \infty, cosa que no es cierta (como bien notás, si a_n \to \infty entonces \displaystyle \sum \frac{a_n}{a_n+1} diverge). Mi sugerencia es que intentes probar que a_n \to 0 sabiendo que \displaystyle \sum \frac{a_n}{a_n+1} converge (pista: el término general de esa serie tiene que tender a 0). Si a_n \to 0, entonces 1+a_n \sim a_n y por lo tanto \displaystyle \frac{a_n}{a_n+1} \sim a_n.

Saludos
En respuesta a Bernardo Marenco

Re: Consulta cuestionario de series

de Valentina Gisel Tejera Luzardo -
Bien! Ahora entiendo mi error. De todos modos si an tiende a cero, entonces an +1 tendería a 1? Si no me equivoco.
De ser así, entiendo por completo el razonamiento y estaría llegando al resultado correcto. Muchísimas gracias por tu tiempo!