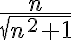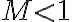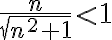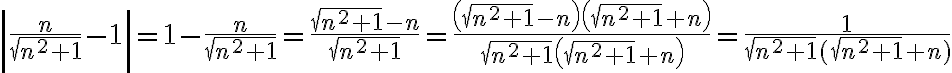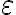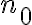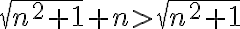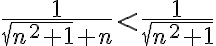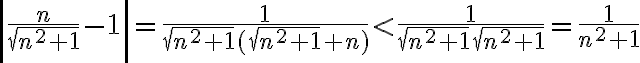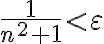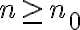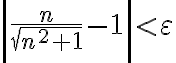Buenas, repasando para el parcial me surgió una duda a cerca de este ejercicio. Sabemos que es una sucesión creciente y que converge a 1, con eso podemos decir que tiene limite, verdad? y que el mismo es 1.
A la hora de probar que el limite es 1 por la def; es decir, que existe un N sub 0 tal que para todo N > a No An esta en el entorno de centro 1 y radio epsilon, queda una ecuación de la siguiente forma: 
la cual estaría teniendo problemas para despejar el No, mi duda es si fallo en las operaciones matemáticas del problema, o si en verdad no hay que probar el limite por la definición cuando ya sabemos que la sucesión converge a 1. (en las soluciones del practico el ejercicio termina diciendo que converge a 1 y no prosigue con el limite.)
Gracias!