Hola tengo una duda con este ejercicio en la parte b cuando demostramos el directo, no se muy bien como ver que existe la sucesión, supuse que no existía y me tomé una creciente y como estaba acotada tenía límite pero no sé cómo ver qué suponiendo que está sucesión creciente tenga límite R con R<L me lleve a un absurdo y así concluir que debe ser L el límite, alguna sugerencia? Gracias
En respuesta a Pedro Manuel Carreras Salaberry
Re: Ejercicio8
Buenas!
En este caso en la demostración del directo se basa en la definición de supremo, tenemos que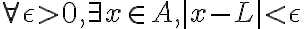 
por ser L el supremo de A, por lo que podemos encontrar para distintos épsilon, elementos de A que estén cada vez más cerca de L y así construimos la sucesión. Además sustituyendo 
por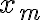 
obtenemos la definición formal de límite. Dejo un dibujito que capaz ayuda a entender la idea de la construcción de la sucesión:
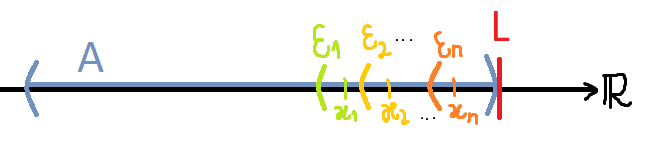
Saludos!
Florencia