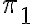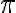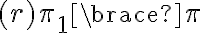Consulta P5 ej.2b

Consulta P5 ej.2b

de Franco Andreoli Brandl -
Número de respuestas: 4

Hola, Bettina.

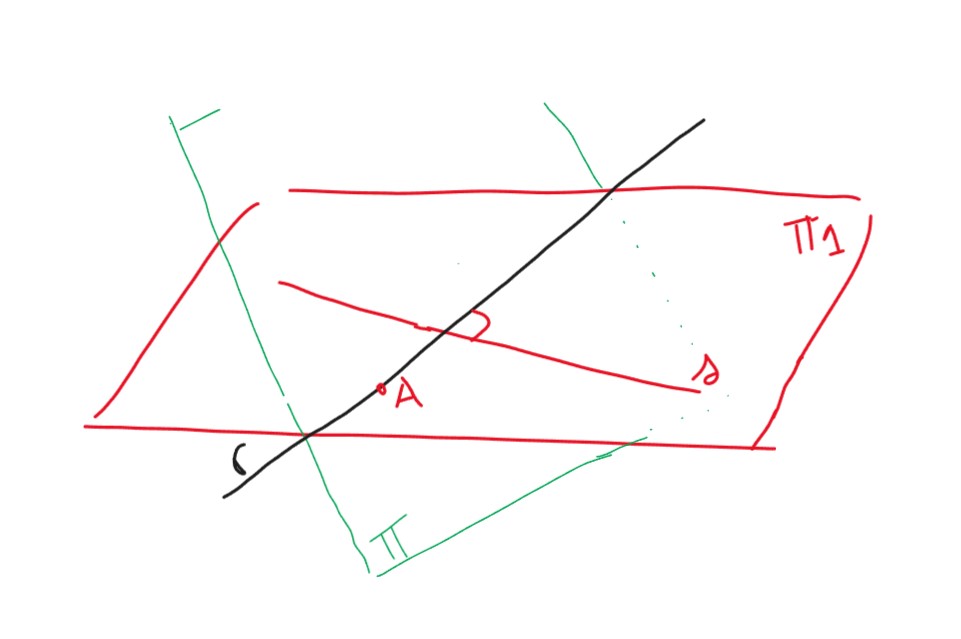
En el ejercicio 2b del P5 nos pide hallar la recta ¨r¨ que pasa por A=(2,1,-1), que está contenida en π) x+2y+3z=1 y es perpendicular a s: x-2z+3=0 , y-z-4=0.

Para esta parte puedo asumir que s esta contenida en un plano paralelo al que contiene a r (esto me garantiza que las normales de cada uno tienen la misma dirección?) y hallar el vector director de r haciendo el producto vectorial entre el vector director de s y la normal del π)? 


En respuesta a Franco Andreoli Brandl

Re: Consulta P5 ej.2b

de Maria Bettina Neira Dutra -
Buenas tardes Franco,

Suponer que s está en un plano paralelo al que contiene r, no es necesario.
Es correcto hallar el vector director de r haciendo el producto vectorial entre la normal del plano y la dirección de s. Si la letra dijera que r y s son ortogonales. 

Cuando pide que dos rectas sean perpendiculares, no solo dicen que sus vectores directores sean perpendiculares, además dice que esas rectas se cortan, es decir, existe la intersección entre las rectas. 

Si dos rectas son perpendiculares, existe un plano que las contiene a ambas, se puede construir un plano  \pi_1 que contenga a la recta s y al punto A.
Por otro lado, la recta r está contenida en el el plano  \pi
Si una recta está contenida en dos planos al mismo tiempo, entonces esa recta se puede obtener como la intersección de ambos planos.
(r) { \pi_1 \brace \pi }  p5-e2b

Si algo no se ve en el mail o no se entiende, hagan clic en "Ver mensaje en su contexto".

Saludos,
Bettina.
En respuesta a Maria Bettina Neira Dutra

Re: Consulta P5 ej.2b

de Franco Andreoli Brandl -
Muchas gracias, quedó clarísimo.

De esto me nace otra duda y es la siguiente; un recta que se cruza perpendicularmente con otra quiere decir entonces que son ortogonales entre ellas? Si así fuese, para la parte c del mismo ejercicio, procedo a armar el plano que contiene a la intersección de s' y r, luego hago el producto vectorial de la normal de ese plano hallado, con el vector director de s que me dice que se cruza perpendicularmente a r y eso me resulta en el vector director de la recta r que busco. Sería correcto?
 
En respuesta a Franco Andreoli Brandl

Re: Consulta P5 ej.2b

de Maria Bettina Neira Dutra -
Correcto. Todo par de rectas perpendiculares, además son ortogonales. Las rectas que se cruzan perpendicularmente son ortogonales, la única condición que se tiene, es que los vectores directores de las rectas, son perpendiculares.

La parte 2c, te queda muy bien resuelta, como la explicas.

Si dos rectas se intersectan, existe un plano que las contiene. Con s' y A te armas un plano, en ese plano sabes que además está r.
Con el producto vectorial de la normal del plano recién hallado y el vector director de s, tenes el vector director de r.
Con el vector director de r y el punto A, tenes la recta r.

Saludos,
Bettina.