Hola, tengo una duda de cómo encarar el ejercicio, debido a que me parece no hay transformador de media ni cuarta onda, entonces debería usar la formula para líneas sin pérdidas? Me confunde qué sería Zx ya que sólo veo dos líneas unidas
gracias
hola,
lo que se pide hallar es la impedancia Zx que se ve desde la izquierda del circuito. usando la expresión de la impedancia vista en función de la "distancia a la carga" (d). hay que tener bien claro "quién es quién" en la fórmula correspondiente, para aplicarla bien. te sugiero primero hallar la impedancia que se ve a 1 metro de la carga (al principio de la línea de impedancia R'0), para luego recién hallar la impedancia Zx, que es la que se e al principio de la línea de impedancia R0.
podés asumir efectivamente que la línea es sin pérdidas. esto es lo que hacemos siempre por defecto.
saludos cordiales,
pablo
Hola, algo así? Lo que hice fue dividirlo en dos partes como planteaste, la distancia que tomé la hice siempre partiendo desde ZL, por eso la primera distancia l es 1m y la segunda es 3m. Primero tomé en cuenta que lo que adaptaba R'o era ZL, y luego lo que adaptaba Ro era el resultado anterior, el cual es la impedancia que se ve desde a, Za. Finalmente, el resultado de eso me debería haber dado la impedancia que se ve desde b, Zx
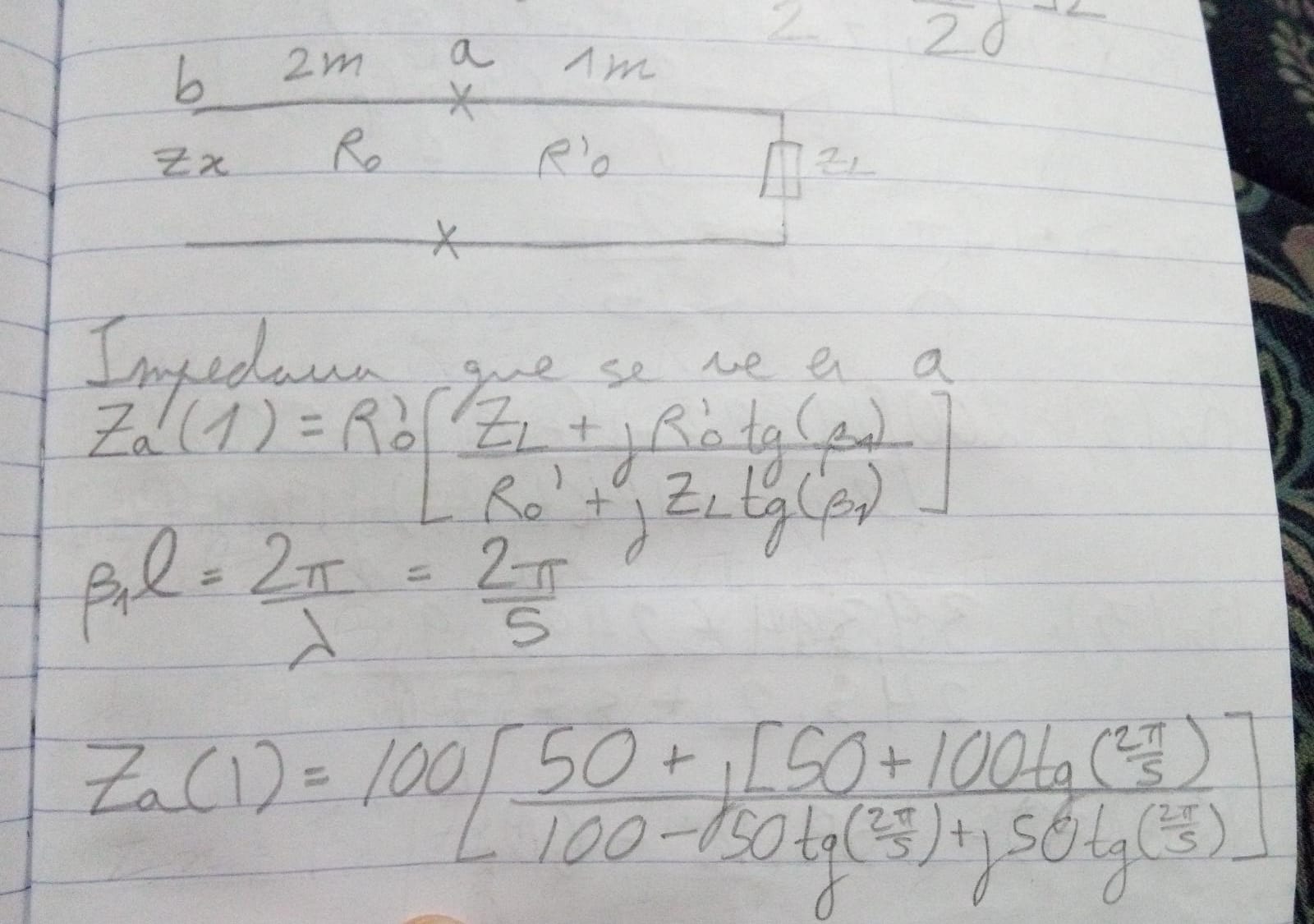
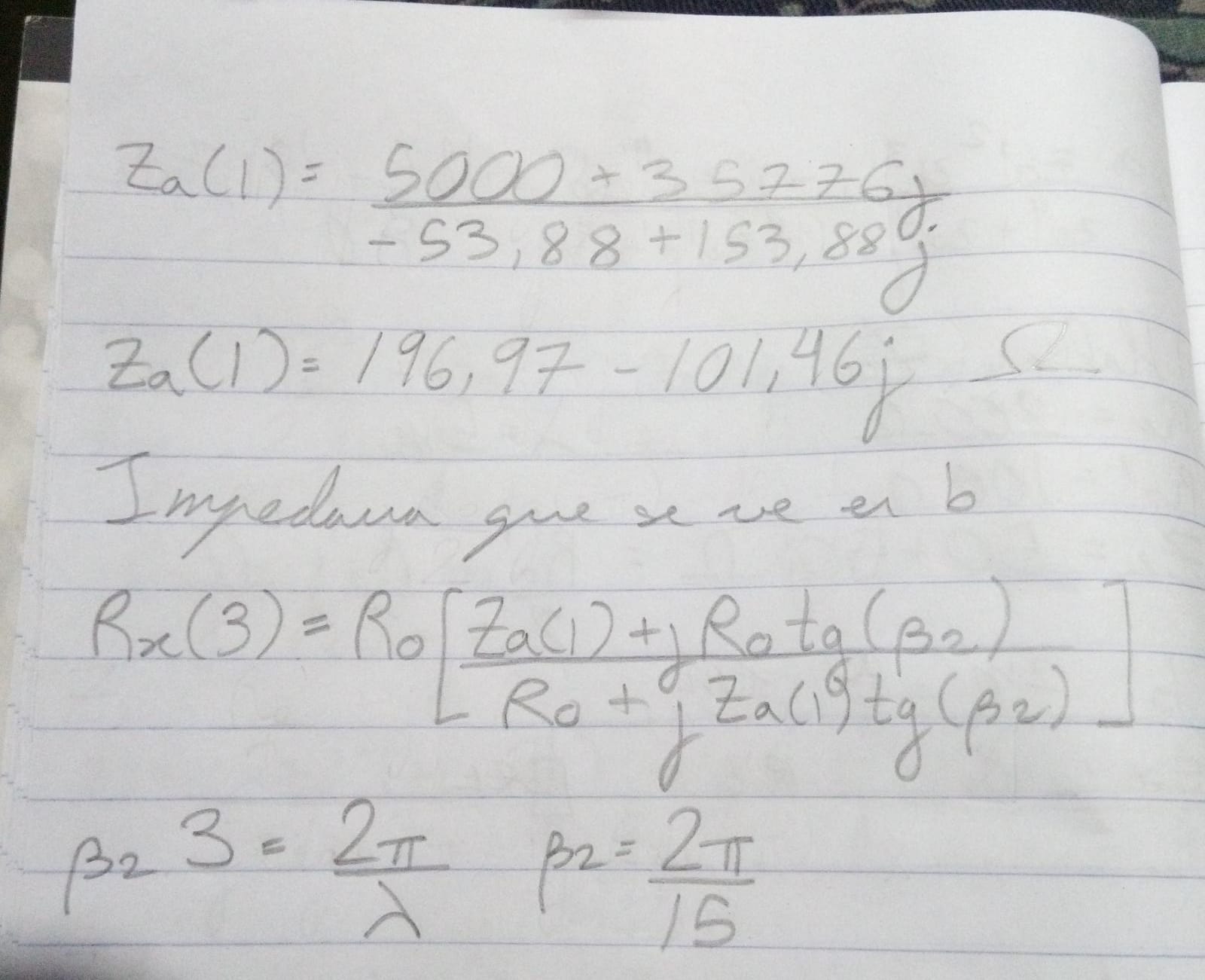
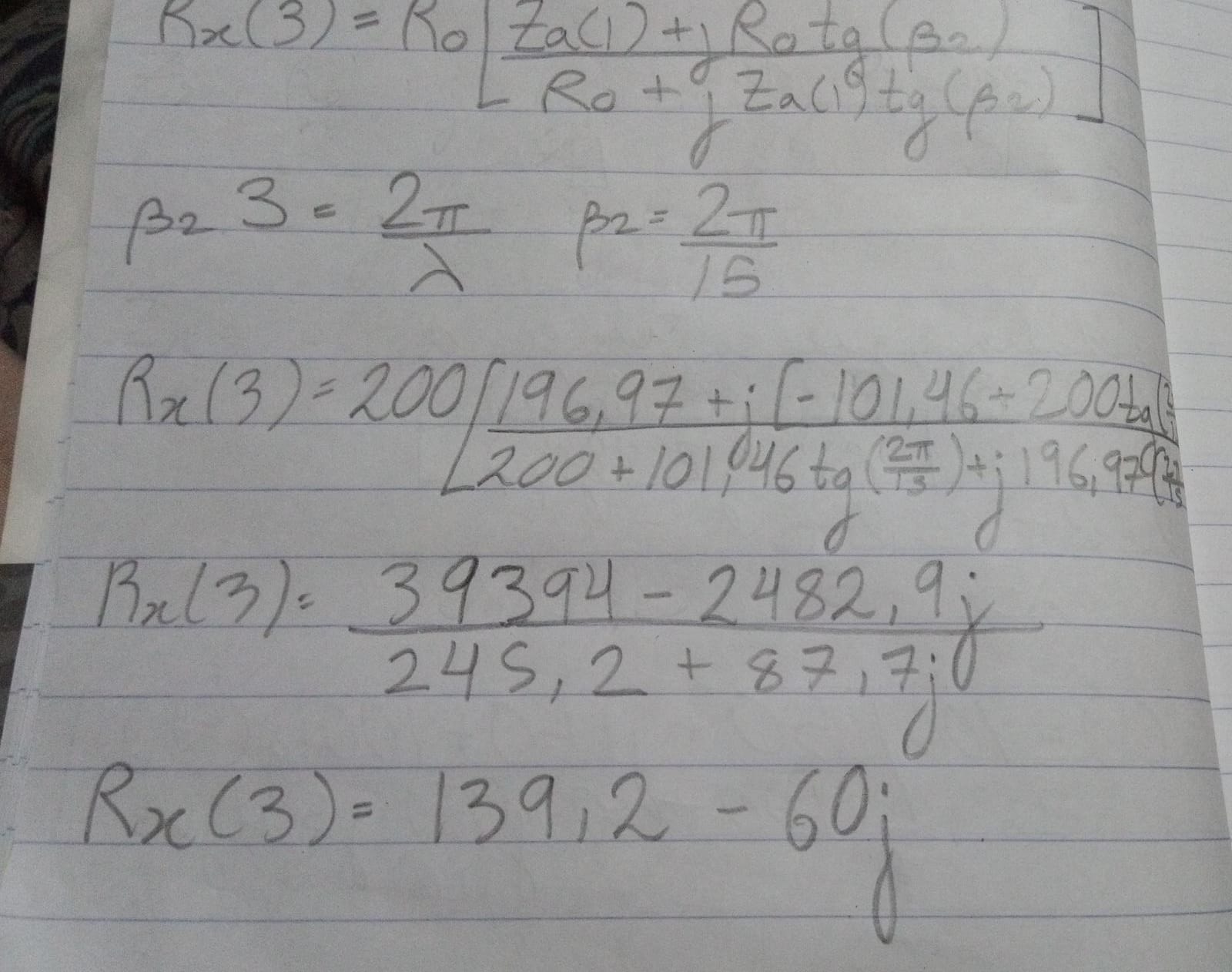
hola,
dos cosas:
- la idea es aplicar la fórmula de la impedancia vista dos veces. la primera vez, la aplicás en la línea de impedancia caracteristica R'0, con la carga RL, y a una idstancia de 1m, así estás en el extremo inicial de la línea. esto de da una nueva impedancia, que es la carga de la línea de impedancia caracteristica R0. con esa nueva impedancia volvés a aplicar la fórmula, ahora con una distancia de 2 m, así estás al principio de la línea.
- me pareció que estás haciendo lío con el argumento de la tangente. tenés que poner tan(\beta.l) y entendí que estás despejando \beta. ojo!! tené en cuenta que el \beta = 2 . \pi / \lambda es dato (en realidad \lambda es dato).
saludos cordiales,
pablo
Hola buenas tardes, realizando el ejercicio en cuestión me encuentro con un resultado de Zbb' = Zaa' (ver archivo adjunto con el gráfico). Entiendo que mi posible error se encuentra en la definición de d =l - z. Le comento como lo pensé, entiendo que l es la longitud total de la línea (3m) y z (que la tomo desde la carga ZL), es 3 - 2 cuando es Z' (Ro') y es 3 - 3 cuando es Z (Ro). Recordé el desarrollo de la compañera y me di cuenta de la diferencia. Por favor comentarme como debería interpretar la toma de los datos 1m y 2m de la línea. Por las dudas, de las notas tome el Z(z) desde ZL.
También aprovecho a consultar si al hallar Zaa', esa es la nueva ZL y por tanto se mueve el eje de ZL hacia Zaa' y es desde ahí donde debo tomar el nuevo d?
Gracias.
Saludos cordiales.
Sebastián.-
También aprovecho a consultar si al hallar Zaa', esa es la nueva ZL y por tanto se mueve el eje de ZL hacia Zaa' y es desde ahí donde debo tomar el nuevo d?
Gracias.
Saludos cordiales.
Sebastián.-
hola,
la Zaa' está bien calculada. y está bien que esa sea la carga de la línea de impedancia característica R0. lo que estás haciando mal es que el largo de esta línea es 2 metros, no 3 metros, por lo que el "d" que tenés que usar en la fórmula es d=2 (en términos de cómo lo escribiste vos, sería l=2, z=0).
saludos,
pablo
la Zaa' está bien calculada. y está bien que esa sea la carga de la línea de impedancia característica R0. lo que estás haciando mal es que el largo de esta línea es 2 metros, no 3 metros, por lo que el "d" que tenés que usar en la fórmula es d=2 (en términos de cómo lo escribiste vos, sería l=2, z=0).
saludos,
pablo
Hola Pablo, buenas tardes, impecable, lo vicho y me vuelvo a comunicar.
Muchas gracias.
Saludos cordiales.
Sebastián.-
Muchas gracias.
Saludos cordiales.
Sebastián.-
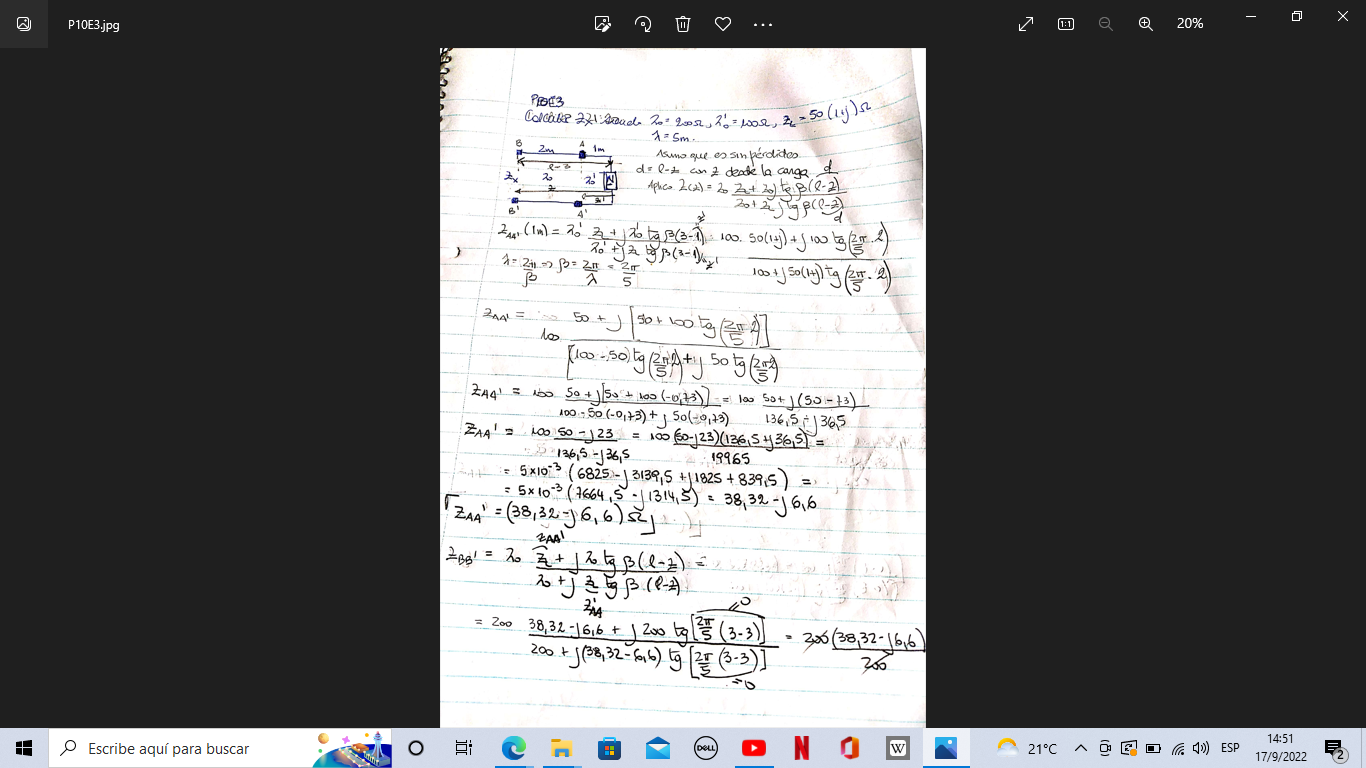
Hola, bunos días. Leyendo el foro vi algunas diferencias entre lo que hicieron mis compañeros y lo que hice yo en este ejercicio, y me parece que hay algo que estoy entendiendo mal, creo que es de dónde se miden las distancias. Adjunto mi resolución del ejercicio y agradecería si me pueden guiar. Saludos.
Hola, te respondo por que creo que yo lo capté: cuando analizas una línea, tienes que ver la carga que está a la derecha de la línea, y cuando aplicas esa fórmula que estás usando, esa te da el resultado que se ve a la izquierda de la línea. O sea,si tienes una línea que sea de ¼ de longitud de onda y haces las cuentas y te da algo tipo Zi= Zl²/Zz, es porque Zz es la impedancia en la izquierda, Zl es la impedancia de la línea y Zi es la impedancia que se ve en el extremo izquierdo de la línea. Esto es porque tomas la distancia que va desde la derecha hasta la izquierda, o sea que la primer distancia si no mal veo sería 1. Haces las cuentas con largo=1. Luego agarras tu resultado y haces las cuentas otra vez y el largo nuevo sera largo=2. El largo es 2 porque tomas desde la izquierda de la linea de impedancia Ro hasta la derecha de ESA línea. Entonces la carga que ves a la derecha tiene la impedancia del Zalgo que hayas calculado antes, mientras que la impedancia a la izquierda de esa línea es Rx lo cual te permite hacer una comparación al final y despejar Rx
Yo la primera me la plantee igual, midiendo la distancia desde la carga ZL. Pero d=l-z (por la ecuación), con l=3m y z=1m me queda que d=2m entonces me cambia el valor de la tangente y de ahí en adelante.
En la segunda parte me quedo todo igual (a menos de ese Zl`), porque medí desde el Zx con un l=2m (y parado en z=0).
hola,
la idea es considerar el circuito:
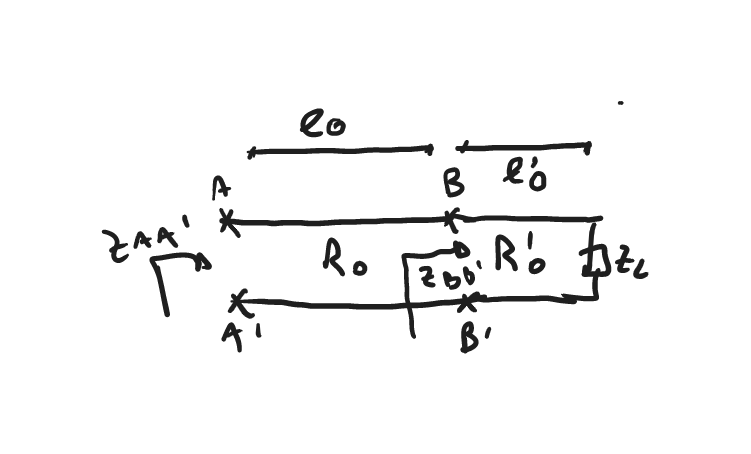
y analizarlo en pasos sucesivos.
1) primero consideramos el circuito "que se ve desde BB'":
acá aplicamos la fórmula que nos devuelve la impedancia vista a una distancia "d" de la carga. lo hacemos con
- d=l'o=1metro
- ZL = ZL
- Z0 = R'0
y obtenemos ZBB'
2) ahora el tramo de línea de impedancia característica R'0, junto con su carga ZL por su equivalente ZBB' y volvemos a aplicar la fórmula. lo hacemos con
- d = l0 = 2m
- ZL = ZBB'
- Z0 = R0
y obtenemos ZAA', que es igual a la Zx que está indicada en la hoja de práctico.
traten de entender bien la fórmula. creo que seguir la deducción aporta bastante.
saludos cordiales,
pablo