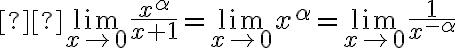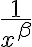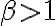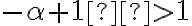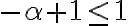Foro Práctico 5

Buenas! 

En este caso la integral impropia es mixta, entonces tenemos que separarla en 2 casos, uno donde tengamos una de primera especia y otro donde tengamos una integral impropia de segunda especie:

$\int_0 ^ \infty \frac{x^\alpha}{x+1}dx = \int_0 ^ 1 \frac{x^\alpha}{x+1}dx + \int_1 ^ \infty \frac{x^\alpha}{x+1}dx$

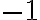Entonces el segundo término es el que no da la condición $\alpha$ mientras que el primero, la integral de segunda especie es el que genera la condición $-1$, para ver esto hacemos el límite de la función que estamos integrando cuanndo 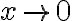$x \rightarrow 0$ para ver a qué es equivalente:

$\lim_{x \rightarrow 0} \frac{x^{\alpha}}{x+1} = \lim_{x \rightarrow 0} x^\alpha = \lim _{x \rightarrow 0} \frac{1}{x^{-\alpha}}$ 

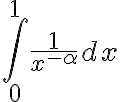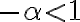Por lo tanto el primer sumando será de la misma clase que $\int _0 ^1 \frac{1}{x^{-\alpha}} dx$ y sabemos que esta integral converge si el exponente al que está elevado $x$ es menor a $1$, por lo que tenemos la condición: $-\alpha < 1$ de donde obtenemos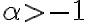 $\alpha > -1$

Si quedan dudas volvé a escribir :)

Saludos!

Florencia