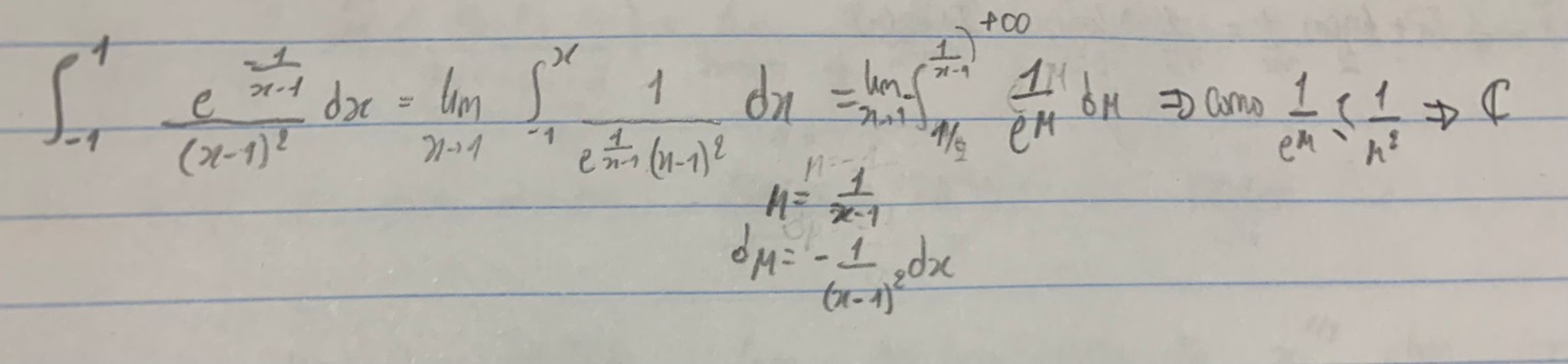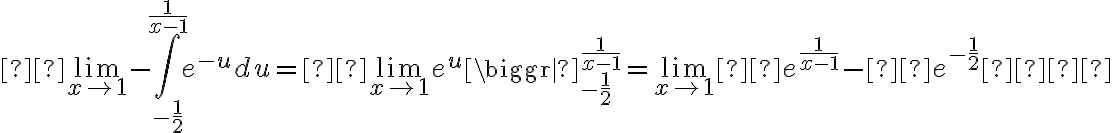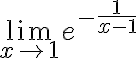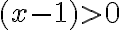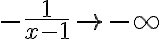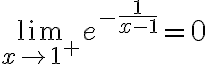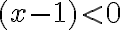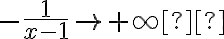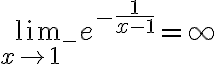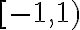6.l

6.l

de Agustín Arístides Almeida Ahlers -
Número de respuestas: 3

Buenas, para este ejercicio apliqué el cambio de variable u=1/x-1 y me quedó la integral de 1/e^u por lo que, aplicando el método de comparación con 1/x^2 me daría que converge pero la respuesta dice que converge, ¿que estaría mal en este procedimiento? la respuesta sugiere emplear el cambio de variable con u=-1/x-1 pero no comprendo porque sería incorrecto tomar este otro camino.

Gracias.6.l

En respuesta a Agustín Arístides Almeida Ahlers

Re: 6.l

de Florencia Uslenghi -
Buenas!
El razonamiento hasta llegar al límite está bien, solo que hay un detalle cuando evaluamos ese límite. Lo que tenemos que calcular es:
 \lim_{x \rightarrow 1} - \int _{ -\frac{1}{2} } ^{ \frac{1}{x-1} } e^{-u} du = \lim_{x \rightarrow 1} e^{u} \biggr | _{ -\frac{1}{2} } ^{ \frac{1}{x-1} } = \lim_{x \rightarrow 1} e^{ \frac{1}{x-1} } - e^{-\frac{1}{2} }   
Para estudiar la convergencia solo nos importa ver si el término \lim_{x \rightarrow 1} e^{ - \frac{1}{x-1} } diverge o da finito. Este límite así planteado no existe porque si nos acercamos por izquierda o por derecha da diferente.
Si nos acercamos por la derecha el término (x-1) > 0 por lo que - \frac{1}{x-1} \rightarrow - \infty entonces:
\lim_{x \rightarrow 1^{+}} e^{ - \frac{1}{x-1} } = 0
Por otro lado si nos acercamos por izquierda  (x-1) < 0 por lo que - \frac{1}{x-1} \rightarrow + \infty  entonces:
\lim_{x \rightarrow 1^{-} } e^{ - \frac{1}{x-1} }= \infty
Ahora solo resta ver si en la integral nos acercamos por derecha o por izquierda, integramos en el intervalo [-1,1) por lo que nos acercamos por izquierda, por ende ese límite diverge y entonces  la integral imporpia que estamos calculando también.
Si quedaron dudas lo volvemos a ver!
Saludos
Florencia