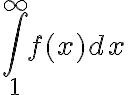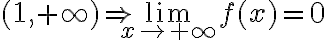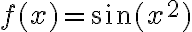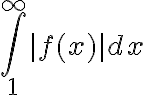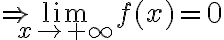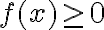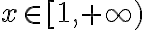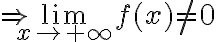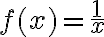CDIVV-2S: Ejercicio cuestionario

Hola, alguien podría ayudarme con este ejercicio? Son 2 versiones distintas del mismo, en la primer imagen la opción III es correcta y en la segunda imagen la opción II es correcta, diría yo que en ambas es por el criterio serie-integral, pero en el resto de las opciones no llego a ninguna conclusión, agradecería si me pueden ayudar.

Re: Ejercicio cuestionario

de Franco Mateo Vienni Baptista - martes, 21 de septiembre de 2021, 15:59

Buenas Martina,

Busquemos algunos contraejemplos:

Si

$\displaystyle \int_1^{\infty}f(x)dx$ converge y

$f$ es derivable en

$(1,+\infty) \Rightarrow \displaystyle \lim_{x \to{+}\infty}{f(x)}=0$ . Un contraejemplo es

$f(x)=\sin(x^2)$

Si

$\displaystyle \int_1^{\infty}|f(x)|dx$ converge

$\Rightarrow \displaystyle \lim_{x \to{+}\infty}{f(x)}=0$ . Un contraejemplo es armarnos una función que valga por ejemplo constante 1 y que cada vez se hagan mas angostos los escalones, lo podes ver explicado en detalle en las notas del curso pagina 47.

Si

$\displaystyle \int_1^{\infty}f(x)dx$ diverge y

$f(x)\geq 0$ para todo

$x\in[1,+\infty)$ y

$f$ es decreciente

$\Rightarrow \displaystyle \lim_{x \to{+}\infty}{f(x)}\neq 0$ . Un contraejemplo es

$f(x)=\dfrac{1}{x}$

Saludos,
Franco.