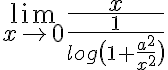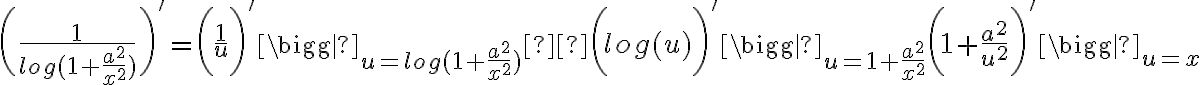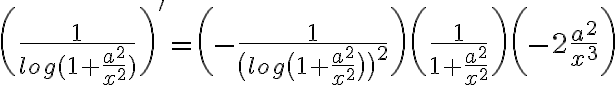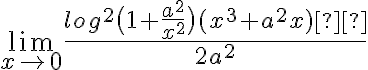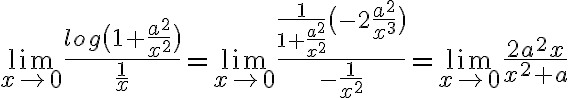Buenas, estoy teniendo problemas para resolver este límite, con x tendiendo a infinito llegué a 0 pero tendiendo a 0 me da que tiende a menos infinito. 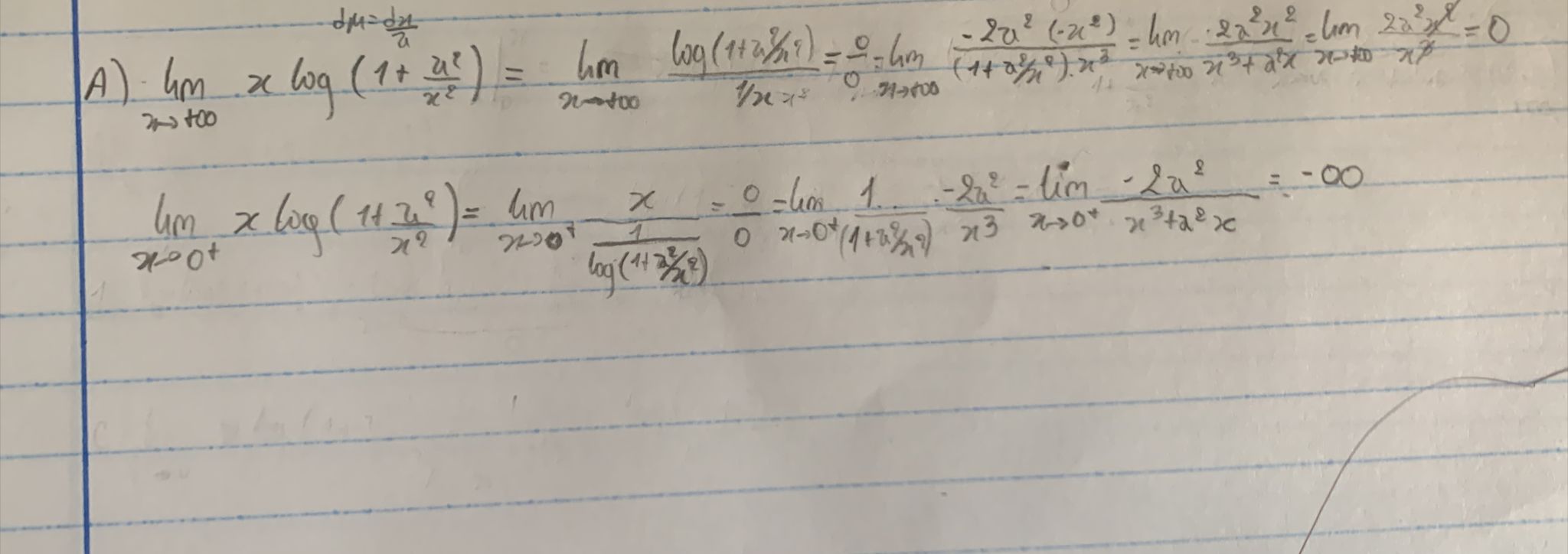
En respuesta a Agustín Arístides Almeida Ahlers
Re: ej 10 (límite aplicando l´Hopital
de Florencia Uslenghi -
Buenas!
En límite cuando 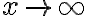 lo calculaste perfecto y para evaluar cuando
lo calculaste perfecto y para evaluar cuando 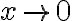 basta con aplicar l'hopital cuando tenés infinito sobre infinito, es decir, como lo tenías expresado en el primer límite.
basta con aplicar l'hopital cuando tenés infinito sobre infinito, es decir, como lo tenías expresado en el primer límite.
No es muy conveniente aplicar l'Hopital dividiendo el logaritmo porque queda una expresión más complicada, vemos como quedaría de esa forma porque me parece que hubo una confusión con la derivada. Queremos calcular el límite:
Al derivar el numerador tenemos un 1, pero la derivada del denominador tenemos la composición de 3 funciones entonces:
Por lo tanto el límite a calcular sería:
Que resulta mucho más complicado que el límite que teníamos antes, sin embargo, podemos plantear lo que habías puesto arriba para 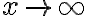 :
:
Saludos!
Florencia
En respuesta a Florencia Uslenghi
Re: ej 10 (límite aplicando l´Hopital
Buenas Florencia, ya me quedo claro, no sabía que tenía la posibilidad de aplicar l´hopital cuando tenés infinito sobre infinito. Muchas gracias!