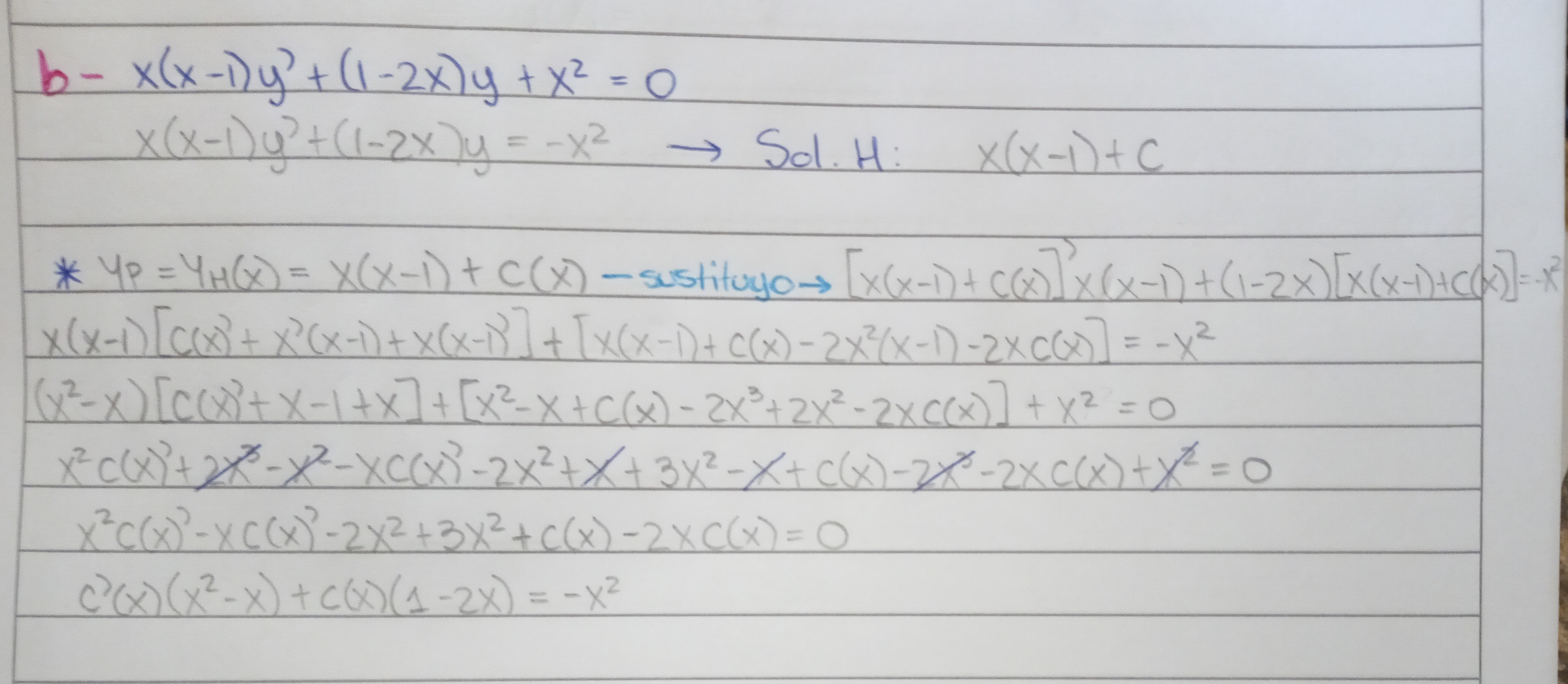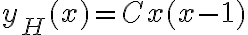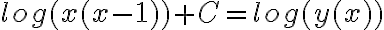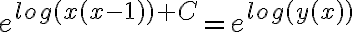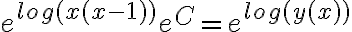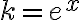Ejercicio 3.b-2

Ejercicio 3.b-2

de Brenda Abigail Tabarez Muniz -
Número de respuestas: 1

Hola, cuando aplico el método de variación de constantes llego a una expresión con C(x) y C'(x). De ahí no sé qué hacer, revisé las cuentas y no encontré errores. Usé el mismo método para el 1, y en ese caso los términos con C(x) se me anularon, y quedaron solo los C'(x) y de ahí integré. 

.

En respuesta a Brenda Abigail Tabarez Muniz

Re: Ejercicio 3.b-2

de Florencia Fernanda Uslenghi Garra -

Buenas!

Lo que hiciste no está mal, el problema está en la solución de la homogénea, que debería ser y_H(x)=Cx(x-1)

Como llegaste a un resultado muy similar me imagino que la confusión estuvo al llegar a este paso:

log(x(x-1)) + C = log(y(x))

Para deshacernos del logaritmo elevamos a ambos lados y obtenemos:

e^{log(x(x-1)) + C} = e^{log(y(x))}

e^{log(x(x-1))}e^{C} = e^{log(y(x))}

Como es una constante cualquiera denominamos k=e^{x} y obtenemos el resultado que mencioné antes. 

Si tenés dudas de los pasos siguientes este ejercicio lo desarrollamos un poco más con otro compañero en el foro CDIVV-2S: Ejercicio 3)b)2) (fing.edu.uy)

Si quedó alguna duda de los pasos anteriores o sobre otra cosa volvé a escribir :)

Saludos!

Florencia