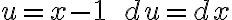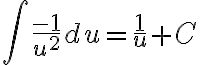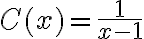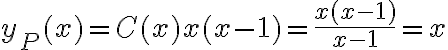Hola, estoy tratando de resolver este ejercicio con el metodo de dimos al fianl de la clase practica de hoy a las 16:30, la cosa es que no la logro escribir como una regla de la multiplicacion de derivadas para hacerle la integral,algun consejo?
En respuesta a Bruno Scanziani Etchebarne
Re: Ejercicio 3)b)2)
Buenas!!
Supongo que estás hablando del método de variación de constantes, cualquier cosa si no es esto a lo que te referís decime y volvemos a verlo.
La homogénea había quedado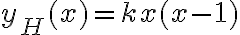 , entonces estamos buscando es una solución particular de la forma:
, entonces estamos buscando es una solución particular de la forma: 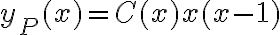 , si derivamos esta expresión tenemos:
, si derivamos esta expresión tenemos: 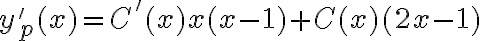 , ahora sustituyendo esto en la ecuación diferencial original tenemos:
, ahora sustituyendo esto en la ecuación diferencial original tenemos:
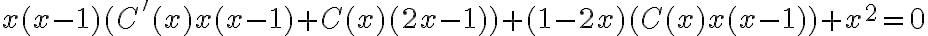
Reordenando queda:
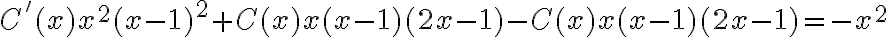
Cancelando los terminos del medio obtenemos:
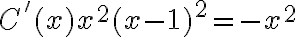
Con esto capaz ayudo, aunque puede que esa no sea tu duda. Cualquier cosa decime :)
Saludos!!
Florencia
Supongo que estás hablando del método de variación de constantes, cualquier cosa si no es esto a lo que te referís decime y volvemos a verlo.
La homogénea había quedado
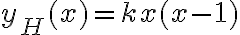 , entonces estamos buscando es una solución particular de la forma:
, entonces estamos buscando es una solución particular de la forma: 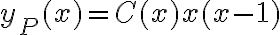 , si derivamos esta expresión tenemos:
, si derivamos esta expresión tenemos: 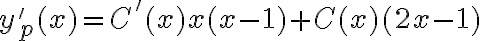 , ahora sustituyendo esto en la ecuación diferencial original tenemos:
, ahora sustituyendo esto en la ecuación diferencial original tenemos: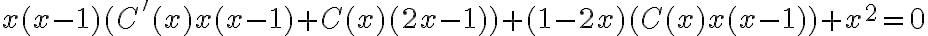
Reordenando queda:
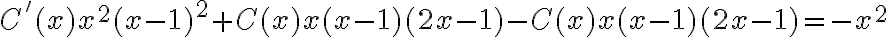
Cancelando los terminos del medio obtenemos:
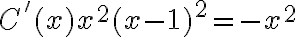
Con esto capaz ayudo, aunque puede que esa no sea tu duda. Cualquier cosa decime :)
Saludos!!
Florencia
En respuesta a Florencia Fernanda Uslenghi Garra
Re: Ejercicio 3)b)2)
Hola, estaba usando otro metodo pero me quedo algo parecido tambien, no se si segui mal pero pase el x² a dividir y despues el (x-1)².
Me quedo Iintegral C′(x) = - integral 1/(x-1)²
No se si hice bien ya que me quedan logaritmos y creo que no es por ahi.
Gracias
Me quedo Iintegral C′(x) = - integral 1/(x-1)²
No se si hice bien ya que me quedan logaritmos y creo que no es por ahi.
Gracias
En respuesta a Bruno Scanziani Etchebarne
Re: Ejercicio 3)b)2)
Buenas tardes!
Saludos!!
Florencia