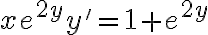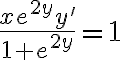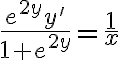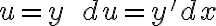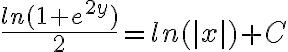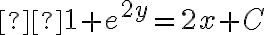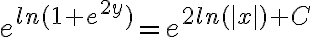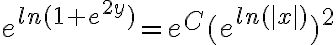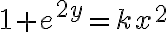Ejercicio 1)c)

Ejercicio 1)c)

de Bruno Scanziani Etchebarne -
Número de respuestas: 6

Hola, alguien me puede dar alguna idea de como encarar el ejercicio lo he intentado de varias maneras y no llego a una solucion.

En respuesta a Bruno Scanziani Etchebarne

Re: Ejercicio 1)c)

de Florencia Fernanda Uslenghi Garra -
Buenas!!
En el ejercicio tenemos que hallar la solución de la ecuación diferencial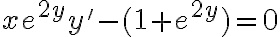 xe^{2y}y'-(1+e^{2y})=0
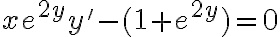
Lo que buscamos cuando aplicamos variables separables es dejar de un lado las cosas que dependen de la variable de la función, en este caso x, y al otro una expresión que dependa de la función y su derivada, con la derivada siempre multiplicando. 
En este caso podemos hacer lo siguiente:
xe^{2y}y'=1+e^{2y}
\frac{xe^{2y}y'}{1+e^{2y}}=1
\frac{e^{2y}y'}{1+e^{2y}}=\frac{1}{x}
\int \frac{e^{2y}y'}{1+e^{2y}} dx = \int \frac{1}{x} dx
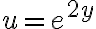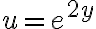La integral de la derecha la sabemos resolver, y para la de la izquierda necesitamos plantear un cambio de variable, podes probar con u=e^{2y}. Si no sale o seguis con dudas volvé a escribir!
Saludos :)
Florencia
En respuesta a Florencia Fernanda Uslenghi Garra

Re: Ejercicio 1)c)

de Chiara Ianira Bianchi Barceló -
Buenas, una pregunta. Por que integramos según dx en ambos términos? Porque vi en vídeos que integral según la variable que tienen (a la izquierda integran según dy y a la derecha según dx)
En respuesta a Florencia Fernanda Uslenghi Garra

Re: Ejercicio 1)c)

de Pedro Gonçalves Schwingel -

hola, llegue a esa solucion pero me dio distinta de las que estan subidas en eva, no logro compreender donde cometi el error

En respuesta a Pedro Gonçalves Schwingel

Re: Ejercicio 1)c)

de Florencia Fernanda Uslenghi Garra -

Buenas!

Lo que hiciste está muy bien, el único problema está en el pasaje: 

\frac{ln(1+e^{2y})}{2} = ln(|x|) + C

 1+e^{2y} = 2x + C

El problema está en el 2x, ya que el dos debería ser el exponente de una e también, es decir, el procedimiento sería:

\frac{ln(1+e^{2y})}{2} = ln(|x|) + C

ln(1+e^{2y}) = 2ln(|x|) + C

e^{ln(1+e^{2y})} = e^{2ln(|x|) + C}

e^{ln(1+e^{2y})} = e^C (e^{ln(|x|)})^2

1+e^{2y} = k x^2

Y siguiendo los mismos pasos desde ahí llegan a la solución. También se podían aplicar las propiedades de logartimo y utilizar que 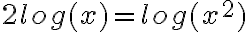2log(x)=log(x^2)

Saludos!!

Florencia :)