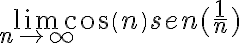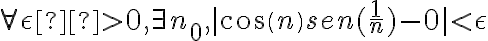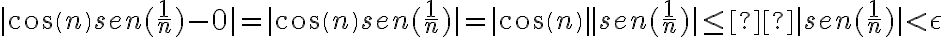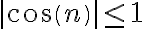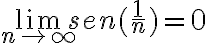Buenas!
Creo que no entendí del todo la duda, en este caso tenemos el límite:
Como comentaste 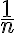 tiende a cero cuando n tiende a infinito por lo que
tiende a cero cuando n tiende a infinito por lo que 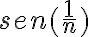 tiende a cero, mientras que
tiende a cero, mientras que 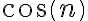 está acotado, por lo que todo este límite tiende a cero.
está acotado, por lo que todo este límite tiende a cero.
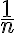 tiende a cero cuando n tiende a infinito por lo que
tiende a cero cuando n tiende a infinito por lo que 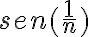 tiende a cero, mientras que
tiende a cero, mientras que 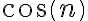 está acotado, por lo que todo este límite tiende a cero.
está acotado, por lo que todo este límite tiende a cero. Por lo tanto analizamos el término: