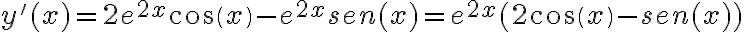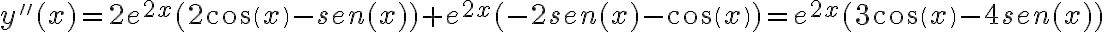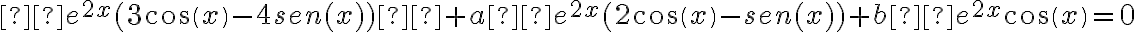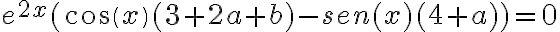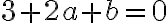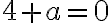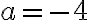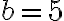Foro Práctico 2

Buenas!

El planteo está bien, lo que hay que hacer para hallar los coeficientes es derivar dos veces la expresión de 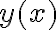$y(x)$ y luego colocarlo en la ecuación original. El tema está en la derivada de la expresión, 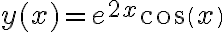$y(x)=e^{2x}cos(x)$ tenemos dos funciones multiplicándose entonces hay que aplicar la regla del producto 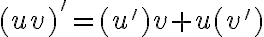$(uv)'=(u')v+u(v')$, así quedaría entonces:

$y'(x) = 2e^{2x}cos(x) - e^{2x}sen(x) = e^{2x} ( 2cos(x) - sen(x) )$

Para la derivada segunda también aplicamos la regla del producto en la expresión de la derecha y nos queda:

$y''(x) = 2 e^{2x} (2cos(x) - sen(x)) + e^{2x} (-2sen(x) - cos(x)) = e^{2x} (3cos(x) - 4sen(x) )$

Ahora colocamos estas expresiones en la ecuación diferencial $y'' + ay' + by = 0$:

$e^{2x} (3cos(x) - 4sen(x))  + a e^{2x} ( 2cos(x) - sen(x) ) + b e^{2x}cos(x) = 0$

Reagrupamos separando en senos y cosenos que son funciones linealmente independientes:

$e^{2x} ( cos(x)(3+2a+b) - sen(x)(4+a)) = 0$

Entonces tenemos que 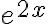$e^{2x}$ no se anula, por lo que el término de la derecha debe ser nulo 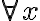$\forall x$, eso significa que tendremos dos ecuaciones:

$3+2a+b=0$

$4+a=0$

De donde sacamos que $a=-4$ y $b=5$

Si quedó alguna duda volve a escribir :)

Saludos!

Florencia