Hola,yo llegue a que el polinomio característico tiene raices (+-) i, y mi solución general sería
e^-x(c1cos(x)+c2sen(x)), no veo claro por que en los resultados simplemente la solución se escribe como c1cos(x)+c2sen(x)? muchas gracias.
Hola,yo llegue a que el polinomio característico tiene raices (+-) i, y mi solución general sería
e^-x(c1cos(x)+c2sen(x)), no veo claro por que en los resultados simplemente la solución se escribe como c1cos(x)+c2sen(x)? muchas gracias.
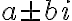 la solución de la homogénea es
la solución de la homogénea es 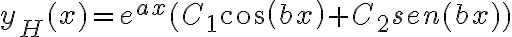 .
. 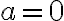 y
y 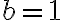 por lo que
por lo que 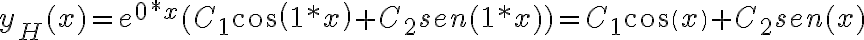
(Editado por Bernardo Marenco - envío original lunes, 22 de agosto de 2022, 16:37)