Ejercicio 2)Parte b

Ejercicio 2)Parte b

de Bruno Scanziani Etchebarne -
Número de respuestas: 5

Hola, estuv intentando resolver este ejercicio y no encuentro la forma de aplicar el ambio de variable que me sugiere, me pueden dar alguna idea.

Gracias

En respuesta a Bruno Scanziani Etchebarne

Re: Ejercicio 2)Parte b

de Bernardo Marenco -

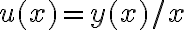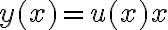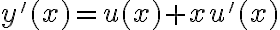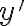Hola Bruno. Fijate que si u(x) = y(x)/x entonces y(x)=u(x)x y y'(x) = u(x) + xu'(x). Entonces, si sustituís y e y' en las ecuaciones por esas expresiones, vas a llegar a una ecuación diferencial en u, que debería quedarte de variables separables y por lo tanto tenés un método para resolverlas. Una vez que halles u, deshacés el cambio de variable y encontrás y.

Saludos
En respuesta a Bernardo Marenco

Re: Ejercicio 2)Parte b

de Pedro Manuel Carreras Salaberry -
Hola, yo tengo una duda con este ejercicio también, cuando sustituyó y despejó la variable, me queda a integrar ((1+u).u')/1-2u-u^2= log(x) pero no sé cómo integrar eso ya que si lo hago por fracciones simples no llego a la solución que está subida
En respuesta a Pedro Manuel Carreras Salaberry

Re: Ejercicio 2)Parte b

de Bernardo Marenco -

Hola. La igualdad que te queda (antes de integrar) es:

\frac{u+1}{-u^2-2u+1} u'=\frac{1}{x} \Rightarrow \frac{u+1}{u^2+2u-1} u'=-\frac{1}{x}

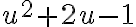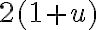Fijate que la derivada de u^2+2u-1 como función de u es 2(1+u), por lo que la integral del término del lado izquierdo es 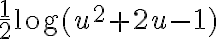\frac12 \log (u^2+2u-1). Así que, luego de integrar, la igualdad de arriba queda:

\frac12 \log (u^2+2u-1) = -\log(x) + K \Rightarrow \log \left(\sqrt{u^2+2u-1}\right) = -\log(x) + c

Tomando exponencial de ambos lados, queda la ecuación:

\sqrt{u^2+2u-1} = \frac{C}{x} \Rightarrow u^2+2u-1 = \frac{K}{x^2} \Rightarrow u^2+2u-1 - \frac{K}{x^2} = 0

Si lo pensás, esa ecuación es un polinomio de grado 2 en u, por lo que podés despejar u usando Bhaskara:

u(x) = \frac{-2 \pm \sqrt{4-4\left(-1 - \frac{K}{x^2}\right)}}{2} = -1 \pm \sqrt{2+\frac{K}{x^2}}

Deshaciendo el cambio de variable deberías llegar a lo mismo que la solución.

Saludos
En respuesta a Bernardo Marenco

Re: Ejercicio 2)Parte b

de Pedro Manuel Carreras Salaberry -
Hola yo cuando derivo 1/2 log(u^2 +2u -1) no me aparece el u'
En respuesta a Pedro Manuel Carreras Salaberry

Re: Ejercicio 2)Parte b

de Florencia Fernanda Uslenghi Garra -
Buenas!
Por las dudas no hay que derivar \frac{log(u^2+2u-1)}{2}.
Para seguir desde acá:
\int \frac{u+1}{u^2+2u-1} u' dx=- \int \frac{1}{x} dx
lo que se hace es aplicar el cambio de variable s=u^2+2u-1 \ \ ds = 2(u+1)u'dx, donde u' aparece por la regla de la cadena porque u es una función. La integral dde la izquierda queda entonces:
\int \frac{1}{2s}ds = \frac{1}{2}log(s) |_{s=u^2+2u-1}
No sé si con esto quedó más claro de donde sale u'
Saludos!