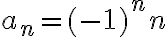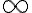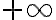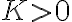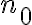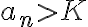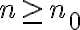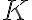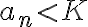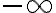Buenas,
Tengo una duda más conceptual que otra cosa. Si una sucesión {an}, cuando n tiende a infinito: oscila entre valores cada vez más grandes positivos y negativos (como si oscilara entre +infinito y -infinito, por decirlo de alguna manera) se considera oscilante o divergente?
Saludos!