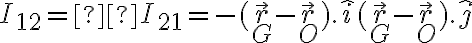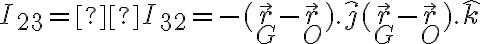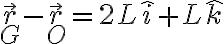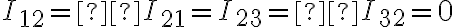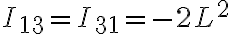Buenas, quería saber bien como es el cálculo para los elementos no diagonales cuando se aplica Steiner para obtener el tensor de inercia desde O. Estaría siendo lo único que no logro entender, osea por qué no son unicamente los términos de distancia entre los ejes principales de G y O los que aparecen ahi. Muchas gracias!
Hola,
De acuerdo con la formula de Steiner, las componentes fuera de la diagonal de la matriz que representa al tensor de Steiner en la base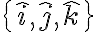 (ordenados de esa forma) serían
(ordenados de esa forma) serían
De acuerdo con la formula de Steiner, las componentes fuera de la diagonal de la matriz que representa al tensor de Steiner en la base
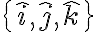 (ordenados de esa forma) serían
(ordenados de esa forma) seríanUsando las fórmulas anteriores tenemos entonces que
Espero que esto responda tu pregunta. De lo contrario no dudes en volver a consultar.
Saludos
Guzmán
Entiendo, muchas gracias!