Hola, Darwin
Esa es una muy buena observación.
Efectivamente, si somos rigurosos con calcular el momento angular respecto a un sistema que se mueve con el centro de masas, deberíamos hacer esa corrección sobre el momento angular de la pelotita. Pero ojo, porque además deberíamos tener en cuenta el momento angular de la barra, que en un sistema que se mueve con el centro de masas, se está trasladando hacia la izquierda con una velocidad igual a la del centro de masas.
El momento angular del sistema antes del choque quedaría entonces de esta forma:

Donde 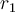 es la distancia entre la pelotita de masa m y el centro de masas del sistema, y
es la distancia entre la pelotita de masa m y el centro de masas del sistema, y 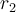 la distancia entre el centro de masas de la barra (lo que en esa clase llamaron punto C) y el centro de masas del sistema.
la distancia entre el centro de masas de la barra (lo que en esa clase llamaron punto C) y el centro de masas del sistema.
Ahora, si hacemos el cálculo de esas posiciones (usando la definición de la posición del centro de masas), podemos ver que:

[Te dejo como ejercicio verificar esas expresiones.]
Sustituyendo en la expresión que teníamos para el momento angular, nos queda:
![\vec{L}_G = \left[ r_1 m v_o - \frac{LM}{2(m+M)}m v_G + \frac{Lm}{2(m+M)}M v_G \right]\hat{k} \vec{L}_G = \left[ r_1 m v_o - \frac{LM}{2(m+M)}m v_G + \frac{Lm}{2(m+M)}M v_G \right]\hat{k}](https://eva.fing.edu.uy/filter/tex/pix.php/b7ec494c0238459e4e26a6202b457089.png)
Donde fijate que los últimos dos términos se cancelan entre sí, quedando el mismo resultado que vieron en clase.
En definitiva, lo que vimos con este desarrollo es que para calcular el momento angular, podemos tomar un punto fijo tal que, en los instantes que estamos considerando (justo antes y justo después del choque) su posición coincida con la posición del centro de masas.
El resultado del momento angular respecto a ese punto fijo, será el mismo que si lo calculáramos respecto a un sistema que se mueve con el centro de masas.
Espero que esto ayude. Cualquier cosa, si algo no quedó claro, volvé a preguntar.
¡Saludos!


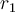
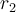

![\vec{L}_G = \left[ r_1 m v_o - \frac{LM}{2(m+M)}m v_G + \frac{Lm}{2(m+M)}M v_G \right]\hat{k} \vec{L}_G = \left[ r_1 m v_o - \frac{LM}{2(m+M)}m v_G + \frac{Lm}{2(m+M)}M v_G \right]\hat{k}](https://eva.fing.edu.uy/filter/tex/pix.php/b7ec494c0238459e4e26a6202b457089.png)